這系列文件到這邊,一直沒有認真討論過座標系統,表面上看來,你至少會接觸兩個座標系統:裁剪空間(Clip Space)與螢幕空間(Screen Space),對 WebGL 來說,螢幕空間指的就是Canvas。
對於直角座標系統來說,你應該遇過幾個不同的表示方式,也就是 X、Y、Z 軸的方向各不相同的表示,不同的軟體或程式庫可能採用不同的方式,這是種困擾,然而,就目前來說 3D 的世界已經是這樣了,你只能試著去分辨它們各自到底採用哪個系統。
粗略來說,座標系統可以分為兩種:左手座標(Left-hand Coordinate)、右手座標(Right-hand Coordinate)。
對於前者,把你的左手拿出來,姆指指向符合 X 軸正方向,食指指向符合 Y 軸正方向,而掌心朝向符合 Z 正方向的話,那該系統就是採用左手座標(怎麼不是用中指?我覺得那好難指!),例如,裁剪空間就是左手座標系統;對於後者,就是把右手拿出來,看看掌心朝向是不是符合 Z 軸正方向,如果是的話,就是採用右手座標系統。
表面上看來,右手座標似乎只是將 Z 軸正方向反過來,不過並非如此,例如,OpenSCAD 是右手座標,然而,它的 X、Y 是代表 2D 平面,Z 代表高度,就視覺上來看,與上面的右手座標三個軸的方向不同。
如果你玩過 OpenSCAD,也許會說,因為 2D 物件會畫在它的 XY 平面上,而 WebGL 裁剪空間的 XY 平面,基本上也是 2D 物件呈現的位置,感覺並不衝突啊?是這樣的嗎?其實 3D 軟體都會有視角,如果是上視圖的話,這種說法就不成立了。
底下是我玩過的幾個與 3D 相關的軟體或程式庫之整理:
你不一定會玩過這些軟體或程式庫,列出這些只是在提醒一件事,使用軟體或程式庫除了左手座標、右手座標之外,還要注意軸代表的意義,特別是在你得進行座標轉換計算的時候。
這系列文件一開始就一直使用裁剪空間,裁剪空間 XYZ 範圍內的頂點與像素會被繪製,雖然 Canvas 繪製時 Y 軸是向下為正,然而,WebGL 會自動處理繪製至螢幕空間的問題,不過,如果你必須得處理像滑鼠點選的問題時,你就必須自行轉換繪圖座標至裁剪空間,在〈使用 attribute 變數〉中,曾經做過這類的事情。
在〈來個 WebGL 程式庫〉中,定義了一些幾何物件,這些物件雖然是採用與裁剪空間相同的左手座標定義,不過這並非必要,也就是說,實際上它是定義在一個獨立的物件空間(Object space),或說是局部空間(Local Space),如果你願意,也可以採用右手座標來定義這個空間。
我們會移動、轉動這些幾何物件,雖然移動時也是採用與裁剪空間相同的左手座標定義,然而這也不是必要的,也就是說,移動、轉動這些幾何物件時,實際上將這些物件中的頂點,轉換至世界空間(World Space),也就是你建構的 3D 世界,如果你願意,也可以採用右手座標來定義這個空間。
世界空間中有許多物件,基於觀察位置、角度、看向的焦點不同,觀察到的畫面也就不同,也就是實際上畫出來的頂點會不同,〈觀察矩陣〉就是用來將頂點座標轉換到觀察空間(View Space),觀察空間得到的座標,再藉由〈正交投影矩陣〉、〈透視投影矩陣〉對應至裁剪空間,這個過程稱為投影。
簡單來說,雖然之前沒談到物件空間、世界空間、觀察空間等,然而這些空間的轉換是隱含在其中的,要能夠順利地繪製出想要的物件,基本上就是這些空間座標的轉換必須順利。
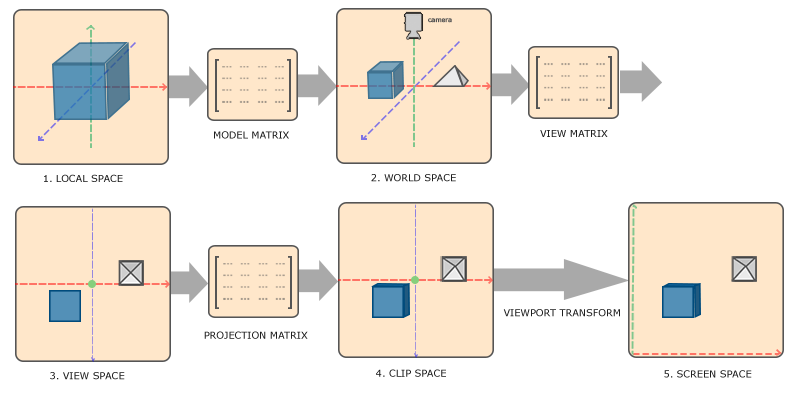
因為 WebGL 是從 OpenGL 衍生而來,因此你在查 WebGL 的文件時,應該會常會看到一些與之相關的 OpenGL 文件,八成你也看過〈Learn OpenGL - Coordinate Systems〉的這張圖,現在應該知道它是怎麼一回事了: