之前談過螺線,像是〈黃金螺線〉、〈阿 基米德螺線〉,我們使用了公式求出每個點,然後連接起來。
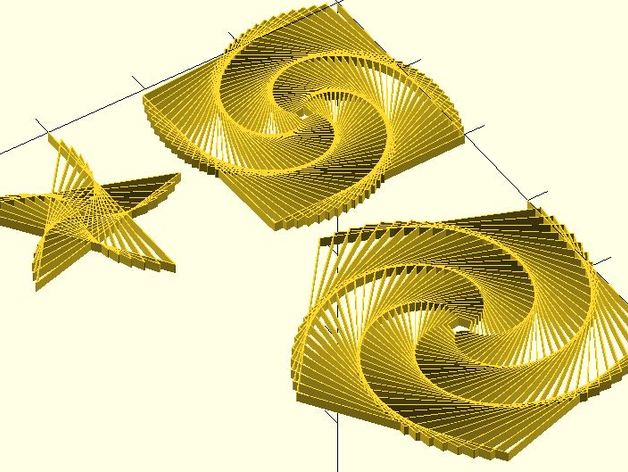
使用海龜的話,也能創造螺線,只要海龜一邊前進、一邊轉動,隨著前進的長度不同、轉動的角度不同,就可以創造出特別的圖樣,Turtle Spiral Generator 就是個例子:
前進與旋轉
海龜螺旋非常地簡單,每次前進的長度是 leng,而後轉動 angle
角度,如果 leng 不變,angle 是 90,那麼畫出來會是正方形,如果 leng
不變,angle 為 120,那麼畫出來會是三角形,如果 leng 不變,angle
為 144,那畫出來會是什麼呢?
function turtle(x, y, angle) = [[x, y], angle];
function get_x(turtle) = turtle[0][0];
function get_y(turtle) = turtle[0][1];
function get_xy(turtle) = turtle[0];
function get_angle(turtle) = turtle[1];
function set_point(turtle, point) = [point, get_angle(turtle)];
function set_x(turtle, x) = [[x, get_y(turtle)], get_angle(turtle)];
function set_y(turtle, y) = [[get_x(turtle), y], get_angle(turtle)];
function set_angle(turtle, angle) = [get_xy(turtle), angle];
function forward(turtle, leng) =
turtle(
get_x(turtle) + leng * cos(get_angle(turtle)),
get_y(turtle) + leng * sin(get_angle(turtle)),
get_angle(turtle)
);
function turn(turtle, angle) = [get_xy(turtle), get_angle(turtle) + angle];
module line(point1, point2, width = 1, cap_round = true) {
angle = 90 - atan((point2[1] - point1[1]) / (point2[0] - point1[0]));
offset_x = 0.5 * width * cos(angle);
offset_y = 0.5 * width * sin(angle);
offset1 = [-offset_x, offset_y];
offset2 = [offset_x, -offset_y];
if(cap_round) {
translate(point1) circle(d = width, $fn = 24);
translate(point2) circle(d = width, $fn = 24);
}
polygon(points=[
point1 + offset1, point2 + offset1,
point2 + offset2, point1 + offset2
]);
}
module polyline(points, width = 1) {
module polyline_inner(points, index) {
if(index < len(points)) {
line(points[index - 1], points[index], width);
polyline_inner(points, index + 1);
}
}
polyline_inner(points, 1);
}
// 以上為之前實作的海龜繪圖
side_leng = 10;
angle = 144;
width = 1;
t1 = turtle(0, 0, 0);
t2 = forward(t1, side_leng);
polyline([get_xy(t1), get_xy(t2)], width);
t3 = forward(turn(t2, angle), side_leng);
polyline([get_xy(t2), get_xy(t3)], width);
t4 = forward(turn(t3, angle), side_leng);
polyline([get_xy(t3), get_xy(t4)], width);
t5 = forward(turn(t4, angle), side_leng);
polyline([get_xy(t4), get_xy(t5)], width);
t6 = forward(turn(t5, angle), side_leng);
polyline([get_xy(t5), get_xy(t6)], width);
結果會是個五芒星,因為它的每個尖角為 36,180 減去 36 就是 144:
來個遞迴
當然,像上面這樣寫其實很差勁,不過,你也不能改成迴圈,因為 OpenSCAD 是 Functional programming 典範,想要能重複進行前進、旋轉,你要使用遞迴:
// 略...
// 以上必須用到先前實作的海龜繪圖
module turtle_spiral(t_before, times, side_leng, angle, width) {
if(times != 0) {
t_after = forward(turn(t_before, angle), side_leng);
polyline([get_xy(t_before), get_xy(t_after)], width);
turtle_spiral(t_after, times - 1, side_leng, angle, width);
}
}
side_leng = 10;
angle = 144;
width = 1;
times = 5;
turtle_spiral(turtle(0, 0, 0), times, side_leng, angle, width);
遞迴看來很難,其實沒什麼,會難其實是你要追蹤太多變數的狀態,通常這代表了你每次遞迴同時做了太多事,在 Imperative programming 風格的程式語言中,你很容易犯下這類的毛病。
然而在 Functional programming 的語言中,進行遞迴反而容易,因為變數或向量等狀態無法變動,這會迫使你寫程式時,一件事一件事來,因而很容易看出重複的模式,就像一開始畫五芒星時,一直重複出現的模式 就是…
t_after = forward(turn(t_before, angle), side_leng);
polyline([get_xy(t_before), get_xy(t_after)], width);
因此,你只要將這個寫在模組中,表示每次只做以上這些事,下一次做什麼?管它呢!直接再呼叫一次模組就是了,當然,我們必須能停止遞迴,在一開
始的五芒星實作中,其實做了五次重複的動作,因此「次數」就是停止的條件,因此後來的 turtle_spiral
模組,多了一個 times 參數,這一次執行表示已經完成一次動作了,因此接下來剩 times
- 1 次動作,這也就是為什麼要 turtle_spiral(t_after, times - 1,
side_leng, angle, width)。
加點變化
除了每次前進固定距離、旋轉固定角度,我們還可以加點變化性,例如,下一次前進時減少 step
長度,並且在前進的長度小於某個長度時,讓海龜停下來:
// 略...
// 以上必須用到先前實作的海龜繪圖
module turtle_spiral(t_before, side_leng, d_step, min_leng, angle, width) {
if(side_leng > min_leng) {
t_after = forward(turn(t_before, angle), side_leng);
polyline([get_xy(t_before), get_xy(t_after)], width);
turtle_spiral(t_after, side_leng - d_step, d_step, min_leng, angle, width);
}
}
side_leng = 50;
d_step = 1;
min_leng = 1;
angle = 90;
width = 1;
turtle_spiral(
turtle(0, 0, 0),
side_leng,
d_step,
min_leng,
angle,
width
);
這會產生什麼結果呢?
感覺很像〈阿基米德螺線〉對吧!事實上,如果你使用以下的參數:
side_leng = 50;
d_step = 0.1;
min_leng = 1;
angle = 15;
width = 1;
無疑地,就是〈阿基米德螺線〉了:
如同〈阿基米德螺線〉中第一個範例,我們每次都是轉固定角度,至
於為什麼臂長會等距?因為每次都減少固定長度,這從剛剛每次轉 90 度的圖,比較容易解釋,從下圖應該可以清楚看到,每個臂長都會是固定的 2d:
從這出發,可以證明在每次轉動的角度不少於 90 的情況下,畫出來的圖案,臂長也都是等距的,自己試試看吧!
你也可以試著調整 side_leng、d_step 等參數,試著找出 Turtle
Spiral Generator 的圖是用哪些參數來構成的。
〈黃金螺線〉使用海龜繪圖的話,也是畫得出來的,不過在每次的前進距離與角 度上比較麻煩一些,我就不解釋了,當成題目讓你試著想想看怎麼做吧!以下我實作的版本:
// 略...
// 以上必須用到先前實作的海龜繪圖
side_leng = 30;
min_leng = 0.2;
angle = 15;
width = 1;
module turtle_spiral_by_times(t_before, times, side_leng, angle, width) {
if(times != 0) {
t_after = forward(turn(t_before, angle), side_leng * angle / 180 * 3.14159);
polyline([get_xy(t_before), get_xy(t_after)], width);
turtle_spiral_by_times(t_after, times - 1, side_leng, angle, width);
} else {
turtle_spiral(t_before, side_leng / 1.618, min_leng, angle, width);
}
}
module turtle_spiral(t_before, side_leng, min_leng, angle, width) {
if(side_leng > min_leng) {
times = 90 / angle;
turtle_spiral_by_times(t_before, 90 / angle, side_leng, angle, width);
}
}
turtle_spiral(
turtle(0, 0, 0),
side_leng,
min_leng,
angle,
width
);
確實是黃金螺線呢!