阿基米德螺線


正如 Spiral moving fish 的簡介中提到的，在發表了 Moving fish 之後，有人提議到，能不能把魚盤起來，這樣就可以有更多魚骨頭了，於是就產生了這個作品了…XD

Spiral moving fish

基本上，盤魚與盤愛心都是類似的：

Text heart chain

從盤愛心中可以看出，我們需要一種縲線，從起始點畫一條直線往外，交到的每個點之間必須是等距的，而阿 基米德螺線就是我們要的。

阿基米德螺線

正如維基百科上談到：

阿基米德螺線（Archimedean spiral） ，亦稱「等速螺線」。當一點P沿動射線OP以等速率運動的同時，這射線又以等角速度繞點O旋轉，點P的軌跡稱為「阿基米德螺線」。它的極坐標方程為: r = a * θ。這種螺線的每條臂的間距永遠相等於 2 * π * a。

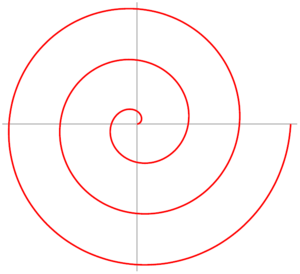
阿基米德螺線

知道公式之後，想要畫出這樣的螺線並不難，要注意的是，θ 是的是徑度而不是角度（而 OpenSCAD 的三角函式是使用角度）：

module line(point1, point2, width = 1, cap_round = true) {
    angle = 90 - atan((point2[1] - point1[1]) / (point2[0] - point1[0]));
    offset_x = 0.5 * width * cos(angle);
    offset_y = 0.5 * width * sin(angle);

    offset1 = [-offset_x, offset_y];
    offset2 = [offset_x, -offset_y];

    if(cap_round) {
        translate(point1) circle(d = width, $fn = 24);
        translate(point2) circle(d = width, $fn = 24);
    }

    polygon(points=[
        point1 + offset1, point2 + offset1,  
        point2 + offset2, point1 + offset2
    ]);
}

module polyline(points, width = 1) {
    module polyline_inner(points, index) {
        if(index < len(points)) {
            line(points[index - 1], points[index], width);
            polyline_inner(points, index + 1);
        }
    }

    polyline_inner(points, 1);
}

PI = 3.14159;
step = 0.25;
circles = 5;
arm_len = 10;

a = arm_len / 2 / PI;
points = [for(theta = [0:step:2 * PI * circles])
    [a * theta * cos(theta * 57.2958), a * theta * sin(theta * 57.2958)]
];

polyline(points, 1);

乍看似乎沒什麼問題：

阿基米德螺線

不過，如果你將 step 設為 1 或者更大的話會如何呢？

阿基米德螺線

咦咦咦？看到了嗎？隨著徑度等量的增加，每個計算出來的座標點與點之間距離會增加，這有什麼問題？如果你只是單純地，想在每個點放個圖案，像是 愛心之類的，愛心之間距離會越來越大，為了簡化，就放個圓來代表好了：

PI = 3.14159;
step = 0.2;
circles = 5;
arm_len = 10;

a = arm_len / 2 / PI;
for(theta = [0:step:2 * PI * circles]) {
    rotate(theta * 57.2958) 
        translate([a * theta, 0, 0]) 
            circle(1, $fn = 24);
}

阿基米德螺線

這樣可不行，我們需要的除了臂長必須相同之外，每個點與點之間距離也必須相同，這樣像愛心鍊這樣的作品，環與環之間才會接得起來。

簡單來說，徑度的增加不可以是等量的，因為徑度越大， r 越大，而同樣的徑度下，越大的 r 弧長就會越長，這也就是為什麼，畫出來的點與點距離會越長的原因。

找出徑度的增量

為了能讓點與點之間等距，我們必須計算出每一次徑度該如何增量，首先整理一下目前的已知：

阿基米德螺線

假設徑度是 Ai 的情況下，臂長會是 Ri = a * Ai，若想要點之間的距 離是 L 的情況下，必須轉動 ad 徑度，那麼得到的臂長會是 R = a * (Ai + ad)，根據餘弦定理，可以寫出 L * L = R * R + Ri * Ri - 2 * R * Ri * cos(ad * 180 / π)（餘弦定理是根據角度），理論上，將 R 代入，就可以試著求出 ad 該是多少。

不過，你可以試著代代看，ad 不好求出來啊！怎麼辦呢？

我的方式是，為了要能盤魚或者是愛心，通常 L 不會很大，也就是 ad 不會很大，ad * a 也就不會很大，也就是說，可以將 R 近似於 Ri， 因此公式就簡化為 L * L = Ri * Ri + Ri * Ri - 2 * Ri * Ri * cos(ad * 180 / π)。

因此就可以求出，ad 會是 acos((2 * Ri * Ri - L * L) / (2 * Ri * Ri)) / 180 * π。

當然，ad 並不會是個固定量，為了要讓點與點之間始終是 L，它會越來越小，知道此 次 ad 值之後，下一次的 Ri，就必須使用 a * (Ai + ad)，以求下一個 ad。

為了要能繪圖，我們一次求出所有的徑度，這是用 find_radians 函式遞迴地求出：

PI = 3.14159;

dots = 100;            // 點的數目
dot_dist = 5;          // 點的距離
arm_len = 5;           // 臂長
init_radian = PI * 4;  // 初始角（第一個點的角）

a = arm_len / 2 / PI;

function r(a, theta) = a * theta;

function radian_step(a, theta, l) = 
    acos((2 * pow(r(a, theta), 2) - pow(l, 2)) / (2 * pow(r(a, theta), 2))) / 180 * PI;

function find_radians(a, l, radians, n, count = 1) =
    count == n ? radians : (
        find_radians(
            a, 
            l, 
            concat(
                radians, // 目前的角度
                [radians[count - 1] + radian_step(a, radians[count - 1], l)] // 轉動後的角度
            ), 
            n,
        count + 1)
    );

for(theta = find_radians(a, dot_dist, [init_radian], dots)) {
    rotate(theta * 57.2958) 
        translate([a * theta, 0, 0]) 
            circle(1, $fn = 24);
}

由於我們是採取近似的方式求值，因此初始角不要太小，誤差才不會大，這對盤魚或愛心之類的已經足夠，上面的程式產生的圖案如下：

阿基米德螺線

如果想要盤某個模型，現在只要將圓替換為該模型，並適當地調整參數就可以了，你想盤什麼呢？來個貪食蛇如何呢？

話說啦！我看了一下 Archimedean spiral generator 中的程式碼，裏頭寫的公式跟這邊的不一樣，我當時一定是從另一個方向導出來，到底是什麼呢？我怎麼也想不起來了，不過這表示，你也可以試著想想 看，有沒有其他方式可以導出別的公式吧！…XD