如果有個函式 f(x, y),給定 x 與 y
的範圍,將之繪製成模型並列印出來,那麼數學函式就不再只是平面上的圖形,而可以是摸得到的實體,那麼數學會不會比較有趣一些?
基本上,對於程式建模來說,這不是難事,看你想做到什麼程度!
最簡單的方式
在每個 [x, y, f(x, y)]
處放上一個小方塊是最簡單的方式,只要方塊夠小,就可以呈現出函式的圖形樣貌,程式也是簡單易懂:
function f(x, y) = (pow(y,2)/pow(2, 2))-(pow(x,2)/pow(2, 2));
min_value = -3;
max_value = 3;
resolution = 0.5;
thickness = 1;
for(x = [min_value:resolution:max_value]) {
for(y = [min_value:resolution:max_value]) {
translate([x, y, f(x, y)])
linear_extrude(thickness, center = true)
square(resolution, center = true);
}
}
resolution 決定了 x 與 y
的步進值,它的值越小,函式圖案就越細緻,當然,繪製的時間就會越久,出來的模型檔案容量就越大。下圖是 resolution
= 0.01 的圖案,在我的電腦上要花上一分多鐘才能計算出預覽圖案:
解析度與模型細緻度本來就是個權衡問題,就算是接下來要介紹的方式,也都有其必須權衡之處,不過,就上面這個方式來說,想要得到更細緻的模型, 耗費的時間成本相對來說,還是比較高一些。
認識 polyhedron
想要建立更細緻的模型,又想試著耗費相對少的成本,可以使用 polyhdedron 模組,在 線
段 中談過 polygon 模組,可以指定頂點與路徑索引來建立多邊形,polyhdedron
模組可說是它的 3D 版本,可用來建立多面體。
雖然 polyhdedron 模組像是 polygon 模組的 3D
版本,不過多面體要考量的比較多,使用上還是比較複雜一些,基本上, polyhdedron
模組背後的使用概念,就是 頂
點索引陣列。
簡單來說,你必須先有多面體的各個頂點,然後為每個頂點編號,接著標示出每個面會用到的頂點編號為何,以 官
方文件的範例 來說,要建立一個與 cube( [ 10, 7, 5 ] )
相同的模型的話,先標上每個頂點編號:
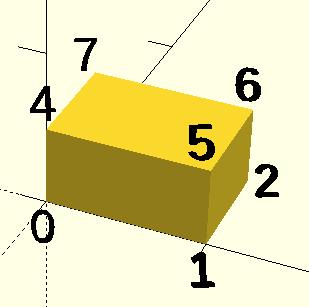
然後找出每個面用了哪些頂點:
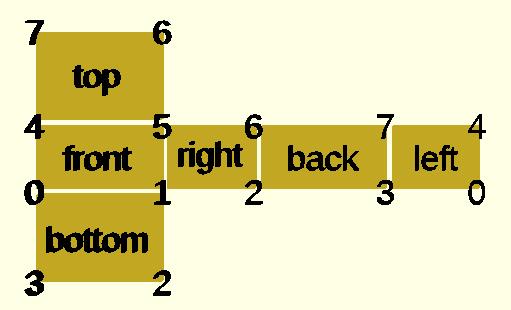
接著使用 polyhedron 模組時,使用向量指定頂點座標,以及每個面的頂點索引:
CubePoints = [
[ 0, 0, 0 ], //0
[ 10, 0, 0 ], //1
[ 10, 7, 0 ], //2
[ 0, 7, 0 ], //3
[ 0, 0, 5 ], //4
[ 10, 0, 5 ], //5
[ 10, 7, 5 ], //6
[ 0, 7, 5 ]]; //7
CubeFaces = [
[0,1,2,3], // bottom
[4,5,1,0], // front
[7,6,5,4], // top
[5,6,2,1], // right
[6,7,3,2], // back
[7,4,0,3]]; // left
polyhedron( CubePoints, CubeFaces );
簡單易懂對吧?不過,稍微改一下範例,改一下頂點 6 的 z 值為 7 呢?
CubePoints = [
[ 0, 0, 0 ], //0
[ 10, 0, 0 ], //1
[ 10, 7, 0 ], //2
[ 0, 7, 0 ], //3
[ 0, 0, 5 ], //4
[ 10, 0, 5 ], //5
[ 10, 7, 7 ], //6
[ 0, 7, 5 ]]; //7
CubeFaces = [
[0,1,2,3], // bottom
[4,5,1,0], // front
[7,6,5,4], // top
[5,6,2,1], // right
[6,7,3,2], // back
[7,4,0,3]]; // left
polyhedron( CubePoints, CubeFaces );
現在索引編號為 4 到 7 的四個點,並不在同一個平面上,就這個簡單的模型來說,OpenSCAD
會試著根據你給定的點與索引,自動為你畫分出兩個三角形,因為任三點一定是在同一平面上(在不平的地面上,三腳椅有其妙用),如果試著 render
也不會出現警訊。
然而,如果有多個 polyhedron 操作下,OpenSCAD 在 render
時似乎會試著合併計算,此時若有多個點不共面,OpenSCAD 在 render 時容易會有以下的警訊:
PolySet has nonplanar faces. Attempting alternate construction
例如以下的這個程式碼就會出現不共面的訊息:
points = [
[0, 0, 1], [1, 0, 2],
[1, 1, 4], [0, 1, 1],
[0, 0, 2], [1, 0, 3],
[1, 1, 5], [0, 1, 2]
];
points2 = [
[1, 0, 2], [2, 0, 2],
[2, 1, 0], [1, 1, 4],
[1, 0, 3], [2, 0, 3],
[2, 1, 1], [1, 1, 5],
];
faces = [
[0,1,2,3], // bottom
[4,5,1,0], // front
[7,6,5,4], // top
[5,6,2,1], // right
[6,7,3,2], // back
[7,4,0,3] // left
];
polyhedron(points, faces);
polyhedron(points2, faces);
只試著執行上面兩個 polyhedron
其中之一並不會有不共面訊息,然而,兩個一起執行時就會,若想解決這類問題,方式是不要依賴 polyhedron
自動為不共面的點切割三角形。
自行切割三角形
對於函式這類的圖形,如果 x、y
是固定遞增,切割三角形就很容易。例如,你有以下的點:
那麼每個點往右與往右上各取一個點,就可以構成三角形:
然後,每個點往右上與往上各取一個點,也可以構成三角形:
這樣就處理完一個方格了,接著就是使用迴圈處理完每個方格:
因此,對於每個 [x, y, f(x, y)] 點,現在劃分為數個三角形了,對於每個三角形,只要每個 f(x,
y) 下降一個厚度值,就可以使用 polyhedron 畫出一個多面體:
當你將所有三角形都如法泡製一番,就可以畫出函式圖形了:
points = [
[[0, 0, 1], [1, 0, 2], [2, 0, 2], [3, 0, 3]],
[[0, 1, 1], [1, 1, 4], [2, 1, 0], [3, 1, 3]],
[[0, 2, 1], [1, 2, 3], [2, 2, 1], [3, 2, 3]],
[[0, 3, 1], [1, 3, 3], [2, 3, 1], [3, 3, 3]]
];
thickness = 1;
faces = [
[0, 1, 2],
[3, 4, 5],
[0, 1, 4, 3],
[1, 2, 5, 4],
[2, 0, 3, 5]
];
z_offset = [0, 0, -thickness];
for(yi = [0:len(points) - 2]) {
for(xi = [0:len(points[yi]) - 2]) {
tri1_top = [
points[yi][xi],
points[yi][xi + 1],
points[yi + 1][xi + 1]
];
tri1_bottom = [
tri1_top[0] + z_offset,
tri1_top[1] + z_offset,
tri1_top[2] + z_offset
];
tri2_top = [
points[yi][xi],
points[yi + 1][xi + 1],
points[yi + 1][xi]
];
tri2_bottom = [
tri2_top[0] + z_offset,
tri2_top[1] + z_offset,
tri2_top[2] + z_offset
];
polyhedron(
points = concat(tri1_top, tri1_bottom),
faces = faces
);
polyhedron(
points = concat(tri2_top, tri2_bottom),
faces = faces
);
}
}
在上面,內建的 concat 函式用來串接兩個向量。實際畫出來的圖案會是:
不過,還是有個問題,實際在 render 時,會出現以下的警訊:
WARNING: Object may not be a valid 2-manifold and may need repair!
這不是我們的程式有問題,而是純綷計算上的一些誤差,使得三角形的面在結合時無法順利閉合,而使得最後 render
時可能產生破面,既然如此,那乾脆用 hull
把這兩個三角形包起來好了,下面這個程式,順便實際產生一個函式圖形:
function f(x, y) = (pow(y,2)/pow(2, 2))-(pow(x,2)/pow(2, 2));
min_value = -3;
max_value = 3;
resolution = 0.5;
thickness = 1;
points = [
for(y = [min_value:resolution:max_value])
[
for(x = [min_value:resolution:max_value])
[x, y, f(x, y)]
]
];
faces = [
[0, 1, 2],
[3, 4, 5],
[0, 1, 4, 3],
[1, 2, 5, 4],
[2, 0, 3, 5]
];
z_offset = [0, 0, -thickness];
for(yi = [0:len(points) - 2]) {
for(xi = [0:len(points[yi]) - 2]) {
tri1_top = [
points[yi][xi],
points[yi][xi + 1],
points[yi + 1][xi + 1]
];
tri1_bottom = [
tri1_top[0] + z_offset,
tri1_top[1] + z_offset,
tri1_top[2] + z_offset
];
tri2_top = [
points[yi][xi],
points[yi + 1][xi + 1],
points[yi + 1][xi]
];
tri2_bottom = [
tri2_top[0] + z_offset,
tri2_top[1] + z_offset,
tri2_top[2] + z_offset
];
// 將兩個三角形包起來,避免誤差產生破面問題
hull() polyhedron(
points = concat(tri1_top, tri1_bottom),
faces = faces
);
hull() polyhedron(
points = concat(tri2_top, tri2_bottom),
faces = faces
);
}
}
跟之前那個簡單方案的圖形比較看看,是不是細緻多了,而且 render 的速度也快上許多:
你可以進一步試著改進這個函式作為練習,例如,想想看,如果想提供函式圖形的骨架的話,要怎麼做呢?

每個三角形是從一個正方形右上往左下切割出來的,你也可以提供選項,供使用者選擇另一個對角線方向:


