一些有規則性的立體圖形,可以使用幾個簡單的變量,並透過運算來產生立體圖形的所有頂點,正多面體正是這麼樣的圖形,只有一個變數就可以定出所有的座標點。
如果將正多面體裝入一個剛好可以容納它的球體中,則正多面體的每一個頂點都會位於球殼上,且每個稜邊長是相等的。正多面體又稱「柏拉圖多面體」,因為希臘哲學家柏拉圖發現,在三維空間中,最多就只有五種正多面體:正四面體、正六面體、正八面體、正十二面體與正二十面體。
如何使用一個變數來指定正多面體的所有頂點呢?先將正多面體的中心置於原點,然後將其中一個頂點置於Y軸上,也就是(0, r, 0),其中從中心至頂點的距離,也就是可以容納正多面體的球半徑,將由Y軸上頂點延伸出來的錂線取出與錂線相接的頂點,再由這些頂點求出對稱原點的另一端 頂點,如此就可以求出所有的頂點。
正四面體、正六面體、正十二面體單一頂點延伸出來的錂線有三條,而正八面體有四條,正二十面體有五條。
正四面體
有一正四面體其中心在原點,如下所示: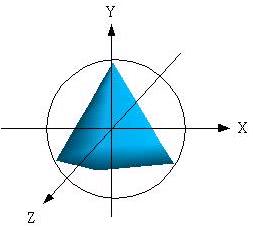
由頂點(0, r, 0)所延伸出來的錂線有三條,為了計算方便,將兩個頂點置於同一XY平面上,所以錂線所接的各頂點經計算後如下所示:
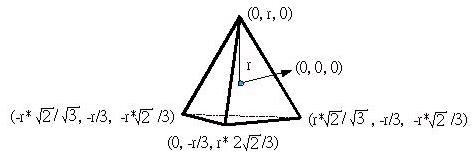
由於正四面體只有四個頂點,所以此時所有的頂點已被訂出,正四面體每個面的頂點數為三,配合頂點索引陣列,可以使用以下的程式來訂出所有的面:
// Java
double sq2 = Math.sqrt(2.0), sq3 = Math.sqrt(3.0);
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, -r/3, r*2*sq2/3);
VETEX[2] = new Point(r*sq2/sq3, -r/3, -r*sq2/3);
VETEX[3] = new Point(-r*sq2/sq3, -r/3, -r*sq2/3);
int[][] V_INDEX = {{0, 1, 2}, {0, 2, 3}, {0, 3, 1}, {1, 3, 2}};
// JavaScript
var sq2 = Math.sqrt(2.0), sq3 = Math.sqrt(3.0);
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, -r/3, r*2*sq2/3);
VETEX[2] = new Point(r*sq2/sq3, -r/3, -r*sq2/3);
VETEX[3] = new Point(-r*sq2/sq3, -r/3, -r*sq2/3);
var V_INDEX = [[0, 1, 2], [0, 2, 3], [0, 3, 1], [1, 3, 2]];
double sq2 = Math.sqrt(2.0), sq3 = Math.sqrt(3.0);
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, -r/3, r*2*sq2/3);
VETEX[2] = new Point(r*sq2/sq3, -r/3, -r*sq2/3);
VETEX[3] = new Point(-r*sq2/sq3, -r/3, -r*sq2/3);
int[][] V_INDEX = {{0, 1, 2}, {0, 2, 3}, {0, 3, 1}, {1, 3, 2}};
// JavaScript
var sq2 = Math.sqrt(2.0), sq3 = Math.sqrt(3.0);
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, -r/3, r*2*sq2/3);
VETEX[2] = new Point(r*sq2/sq3, -r/3, -r*sq2/3);
VETEX[3] = new Point(-r*sq2/sq3, -r/3, -r*sq2/3);
var V_INDEX = [[0, 1, 2], [0, 2, 3], [0, 3, 1], [1, 3, 2]];
正六面體
有一正六面體其中心在原點,如下所示: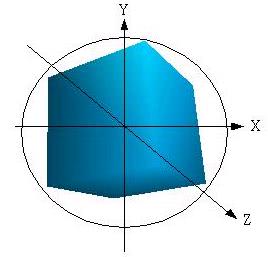
由頂點(0, r, 0)所延伸出來的錂線有三條,為了計算方便,將兩個頂點置於同一XY平面上,所以錂線所接的各頂點經計算後如下所示:
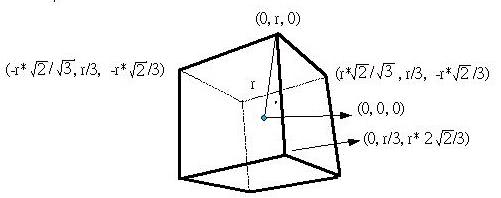
其它未定出的頂點皆以原點對稱於這四個頂點,對稱於原點其實就是將(x, y, z)都乘上負號,假設有個方法是minus()是進行這項工作,則其它頂點的計算及面的索引陣列如下所示,其中NVT表示頂點數,對正六面體而言是8:
// Java
double sq2 = Math.sqrt(2.0), sq3 = Math.sqrt(3.0);
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, r/3, r*2*sq2/3);
VETEX[2] = new Point(r*sq2/sq3, r/3, -r*sq2/3);
VETEX[3] = new Point(-r*sq2/sq3, r/3, -r*sq2/3);
for(int i = 0; i < NVT; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
int[][] V_INDEX = {{0, 1, 7, 2}, {0, 2, 5, 3}, {0, 3, 6, 1},
{4, 6, 3, 5}, {4, 7, 1, 6}, {4, 5, 2, 7}};
// JavaScript
var sq2 = Math.sqrt(2.0), sq3 = Math.sqrt(3.0);
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, r/3, r*2*sq2/3);
VETEX[2] = new Point(r*sq2/sq3, r/3, -r*sq2/3);
VETEX[3] = new Point(-r*sq2/sq3, r/3, -r*sq2/3);
for(var i = 0; i < NVT; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
var V_INDEX = [[0, 1, 7, 2], [0, 2, 5, 3], [0, 3, 6, 1],
[4, 6, 3, 5], [4, 7, 1, 6], [4, 5, 2, 7]];
double sq2 = Math.sqrt(2.0), sq3 = Math.sqrt(3.0);
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, r/3, r*2*sq2/3);
VETEX[2] = new Point(r*sq2/sq3, r/3, -r*sq2/3);
VETEX[3] = new Point(-r*sq2/sq3, r/3, -r*sq2/3);
for(int i = 0; i < NVT; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
int[][] V_INDEX = {{0, 1, 7, 2}, {0, 2, 5, 3}, {0, 3, 6, 1},
{4, 6, 3, 5}, {4, 7, 1, 6}, {4, 5, 2, 7}};
// JavaScript
var sq2 = Math.sqrt(2.0), sq3 = Math.sqrt(3.0);
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, r/3, r*2*sq2/3);
VETEX[2] = new Point(r*sq2/sq3, r/3, -r*sq2/3);
VETEX[3] = new Point(-r*sq2/sq3, r/3, -r*sq2/3);
for(var i = 0; i < NVT; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
var V_INDEX = [[0, 1, 7, 2], [0, 2, 5, 3], [0, 3, 6, 1],
[4, 6, 3, 5], [4, 7, 1, 6], [4, 5, 2, 7]];
正八面體
依以上同樣的道理,可以定出正八面體的一組基本頂點,不過正八面體的中心的三個頂點可以調整至XYZ三軸上,如下所示: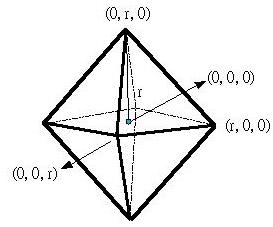
正八面體的頂點配置方式與頂點索引陣列,提供以下的程式作參考,其中NVT表示頂點數,對正八面體而言是6:
// Java
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, 0, r);
VETEX[2] = new Point(r, 0, 0);
for(int i = 0; i < NVT; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
int[][] V_INDEX = {{0, 1, 2}, {0, 2, 4}, {0, 4, 5}, {0, 5, 1},
{3, 5, 4}, {3, 1, 5}, {3, 2, 1}, {3, 4, 2}};
// JavaScript
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, 0, r);
VETEX[2] = new Point(r, 0, 0);
for(var i = 0; i < NVT; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
var V_INDEX = [[0, 1, 2], [0, 2, 4], [0, 4, 5], [0, 5, 1],
[3, 5, 4], [3, 1, 5], [3, 2, 1], [3, 4, 2]];
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, 0, r);
VETEX[2] = new Point(r, 0, 0);
for(int i = 0; i < NVT; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
int[][] V_INDEX = {{0, 1, 2}, {0, 2, 4}, {0, 4, 5}, {0, 5, 1},
{3, 5, 4}, {3, 1, 5}, {3, 2, 1}, {3, 4, 2}};
// JavaScript
VETEX[0] = new Point(0, r, 0);
VETEX[1] = new Point(0, 0, r);
VETEX[2] = new Point(r, 0, 0);
for(var i = 0; i < NVT; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
var V_INDEX = [[0, 1, 2], [0, 2, 4], [0, 4, 5], [0, 5, 1],
[3, 5, 4], [3, 1, 5], [3, 2, 1], [3, 4, 2]];
正十二面體
下圖為正十二面體的圖形: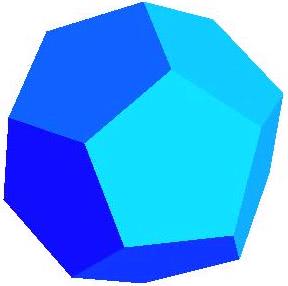
正十二面體的對稱頂點有十對,頂點配置與頂點索引陣列如下所示,其中NVT表示頂點數,對正十二面體而言是20:
// Java
double sq3=Math.sqrt(3.0),sq5=Math.sqrt(5.0);
VETEX[0] = new Point(0,r,0);
VETEX[1] = new Point(0,r*sq5/3,r*2/3);
VETEX[2] = new Point(r*sq3/3,r*sq5/3,-r/3);
VETEX[3] = new Point(-r*sq3/3,r*sq5/3,-r/3);
VETEX[4] = new Point(r*sq3/3,r/3,r*sq5/3);
VETEX[5] = new Point(r*t1*sq3/3,r/3,r*t2*t2/3);
VETEX[6] = new Point(r*t2*sq3/3,r/3,-r*t1*t1/3);
VETEX[7] = new Point(-r*t2*sq3/3,r/3,-r*t1*t1/3);
VETEX[8] = new Point(-r*t1*sq3/3,r/3,r*t2*t2/3);
VETEX[9] = new Point(-r*sq3/3,r/3,r*sq5/3);
for(int i = 0; i < NVT/2; i++) {
VETEX[NVT/2+i] = VETEX(Vt[i]);
}
int[][] V_INDEX =
{{ 0, 1, 4, 5, 2},{ 0, 2, 6, 7, 3},{ 0, 3, 8, 9, 1},
{ 1, 9,16,17, 4},{ 2, 5,18,19, 6},{ 3, 7,14,15, 8},
{10,12,15,14,11},{10,13,17,16,12},{10,11,19,18,13},
{11,14, 7, 6,19},{12,16, 9, 8,15},{13,18, 5, 4,17}};
// JavaScript
var sq3=Math.sqrt(3.0),sq5=Math.sqrt(5.0);
VETEX[0] = new Point(0,r,0);
VETEX[1] = new Point(0,r*sq5/3,r*2/3);
VETEX[2] = new Point(r*sq3/3,r*sq5/3,-r/3);
VETEX[3] = new Point(-r*sq3/3,r*sq5/3,-r/3);
VETEX[4] = new Point(r*sq3/3,r/3,r*sq5/3);
VETEX[5] = new Point(r*t1*sq3/3,r/3,r*t2*t2/3);
VETEX[6] = new Point(r*t2*sq3/3,r/3,-r*t1*t1/3);
VETEX[7] = new Point(-r*t2*sq3/3,r/3,-r*t1*t1/3);
VETEX[8] = new Point(-r*t1*sq3/3,r/3,r*t2*t2/3);
VETEX[9] = new Point(-r*sq3/3,r/3,r*sq5/3);
for(var i = 0; i < NVT/2; i++) {
VETEX[NVT/2+i] = VETEX(Vt[i]);
}
var V_INDEX =
[[ 0, 1, 4, 5, 2],[ 0, 2, 6, 7, 3],[ 0, 3, 8, 9, 1],
[ 1, 9,16,17, 4],[ 2, 5,18,19, 6],[ 3, 7,14,15, 8],
[10,12,15,14,11],[10,13,17,16,12],[10,11,19,18,13],
[11,14, 7, 6,19],[12,16, 9, 8,15],[13,18, 5, 4,17]];
double sq3=Math.sqrt(3.0),sq5=Math.sqrt(5.0);
VETEX[0] = new Point(0,r,0);
VETEX[1] = new Point(0,r*sq5/3,r*2/3);
VETEX[2] = new Point(r*sq3/3,r*sq5/3,-r/3);
VETEX[3] = new Point(-r*sq3/3,r*sq5/3,-r/3);
VETEX[4] = new Point(r*sq3/3,r/3,r*sq5/3);
VETEX[5] = new Point(r*t1*sq3/3,r/3,r*t2*t2/3);
VETEX[6] = new Point(r*t2*sq3/3,r/3,-r*t1*t1/3);
VETEX[7] = new Point(-r*t2*sq3/3,r/3,-r*t1*t1/3);
VETEX[8] = new Point(-r*t1*sq3/3,r/3,r*t2*t2/3);
VETEX[9] = new Point(-r*sq3/3,r/3,r*sq5/3);
for(int i = 0; i < NVT/2; i++) {
VETEX[NVT/2+i] = VETEX(Vt[i]);
}
int[][] V_INDEX =
{{ 0, 1, 4, 5, 2},{ 0, 2, 6, 7, 3},{ 0, 3, 8, 9, 1},
{ 1, 9,16,17, 4},{ 2, 5,18,19, 6},{ 3, 7,14,15, 8},
{10,12,15,14,11},{10,13,17,16,12},{10,11,19,18,13},
{11,14, 7, 6,19},{12,16, 9, 8,15},{13,18, 5, 4,17}};
// JavaScript
var sq3=Math.sqrt(3.0),sq5=Math.sqrt(5.0);
VETEX[0] = new Point(0,r,0);
VETEX[1] = new Point(0,r*sq5/3,r*2/3);
VETEX[2] = new Point(r*sq3/3,r*sq5/3,-r/3);
VETEX[3] = new Point(-r*sq3/3,r*sq5/3,-r/3);
VETEX[4] = new Point(r*sq3/3,r/3,r*sq5/3);
VETEX[5] = new Point(r*t1*sq3/3,r/3,r*t2*t2/3);
VETEX[6] = new Point(r*t2*sq3/3,r/3,-r*t1*t1/3);
VETEX[7] = new Point(-r*t2*sq3/3,r/3,-r*t1*t1/3);
VETEX[8] = new Point(-r*t1*sq3/3,r/3,r*t2*t2/3);
VETEX[9] = new Point(-r*sq3/3,r/3,r*sq5/3);
for(var i = 0; i < NVT/2; i++) {
VETEX[NVT/2+i] = VETEX(Vt[i]);
}
var V_INDEX =
[[ 0, 1, 4, 5, 2],[ 0, 2, 6, 7, 3],[ 0, 3, 8, 9, 1],
[ 1, 9,16,17, 4],[ 2, 5,18,19, 6],[ 3, 7,14,15, 8],
[10,12,15,14,11],[10,13,17,16,12],[10,11,19,18,13],
[11,14, 7, 6,19],[12,16, 9, 8,15],[13,18, 5, 4,17]];
正二十面體
下圖為正二十面體的圖形:
正二十面體的對稱頂點有六對,頂點配置與頂點索引陣列如下所示,其中NVT表示頂點數,對正二十面體而言是12:
// Java
double sq5=Math.sqrt(5.0);
double t1 = (sq5+1)/2, t2 = (sq5-1)/2;
VETEX[0] = new Point(0,r,0);
VETEX[1] = new Point(0,r/sq5,r*2/sq5);
VETEX[2] = new Point(r*Math.sqrt(t1/sq5),r/sq5,r*t2/sq5);
VETEX[3] = new Point(r*Math.sqrt(t2/sq5),r/sq5,-r*t1/sq5);
VETEX[4] = new Point(-r*Math.sqrt(t2/sq5),r/sq5,-r*t1/sq5);
VETEX[5] = new Point(-r*Math.sqrt(t1/sq5),r/sq5,r*t2/sq5);
for(int i = 0; i<NVT/2; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
int[][] V_INDEX =
{{0, 1,2},{0, 2,3},{0, 3,4},{ 0, 4, 5},{ 0,5, 1},
{1,10,2},{2,11,3},{3, 7,4},{ 4, 8, 5},{ 5,9, 1},
{6, 8,7},{6, 9,8},{6,10,9},{ 6,11,10},{ 6,7,11},
{7, 8,4},{8, 9,5},{9,10,1},{10,11, 2},{11,7, 3}};
// JavaScript
var sq5=Math.sqrt(5.0);
var t1 = (sq5+1)/2, t2 = (sq5-1)/2;
VETEX[0] = new Point(0,r,0);
VETEX[1] = new Point(0,r/sq5,r*2/sq5);
VETEX[2] = new Point(r*Math.sqrt(t1/sq5),r/sq5,r*t2/sq5);
VETEX[3] = new Point(r*Math.sqrt(t2/sq5),r/sq5,-r*t1/sq5);
VETEX[4] = new Point(-r*Math.sqrt(t2/sq5),r/sq5,-r*t1/sq5);
VETEX[5] = new Point(-r*Math.sqrt(t1/sq5),r/sq5,r*t2/sq5);
for(var i = 0; i<NVT/2; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
var V_INDEX =
[[0, 1,2],[0, 2,3],[0, 3,4],[ 0, 4, 5],[ 0,5, 1],
[1,10,2],[2,11,3],[3, 7,4],[ 4, 8, 5],[ 5,9, 1],
[6, 8,7],[6, 9,8],[6,10,9],[ 6,11,10],[ 6,7,11],
[7, 8,4],[8, 9,5],[9,10,1],[10,11, 2],[11,7, 3]];
double sq5=Math.sqrt(5.0);
double t1 = (sq5+1)/2, t2 = (sq5-1)/2;
VETEX[0] = new Point(0,r,0);
VETEX[1] = new Point(0,r/sq5,r*2/sq5);
VETEX[2] = new Point(r*Math.sqrt(t1/sq5),r/sq5,r*t2/sq5);
VETEX[3] = new Point(r*Math.sqrt(t2/sq5),r/sq5,-r*t1/sq5);
VETEX[4] = new Point(-r*Math.sqrt(t2/sq5),r/sq5,-r*t1/sq5);
VETEX[5] = new Point(-r*Math.sqrt(t1/sq5),r/sq5,r*t2/sq5);
for(int i = 0; i<NVT/2; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
int[][] V_INDEX =
{{0, 1,2},{0, 2,3},{0, 3,4},{ 0, 4, 5},{ 0,5, 1},
{1,10,2},{2,11,3},{3, 7,4},{ 4, 8, 5},{ 5,9, 1},
{6, 8,7},{6, 9,8},{6,10,9},{ 6,11,10},{ 6,7,11},
{7, 8,4},{8, 9,5},{9,10,1},{10,11, 2},{11,7, 3}};
// JavaScript
var sq5=Math.sqrt(5.0);
var t1 = (sq5+1)/2, t2 = (sq5-1)/2;
VETEX[0] = new Point(0,r,0);
VETEX[1] = new Point(0,r/sq5,r*2/sq5);
VETEX[2] = new Point(r*Math.sqrt(t1/sq5),r/sq5,r*t2/sq5);
VETEX[3] = new Point(r*Math.sqrt(t2/sq5),r/sq5,-r*t1/sq5);
VETEX[4] = new Point(-r*Math.sqrt(t2/sq5),r/sq5,-r*t1/sq5);
VETEX[5] = new Point(-r*Math.sqrt(t1/sq5),r/sq5,r*t2/sq5);
for(var i = 0; i<NVT/2; i++) {
VETEX[NVT/2+i] = minus(VETEX[i]);
}
var V_INDEX =
[[0, 1,2],[0, 2,3],[0, 3,4],[ 0, 4, 5],[ 0,5, 1],
[1,10,2],[2,11,3],[3, 7,4],[ 4, 8, 5],[ 5,9, 1],
[6, 8,7],[6, 9,8],[6,10,9],[ 6,11,10],[ 6,7,11],
[7, 8,4],[8, 9,5],[9,10,1],[10,11, 2],[11,7, 3]];
由以上,只要一個變數r,就可以訂出所有的正多面體頂點,當然所犧牲的就是一些運算時間了。

