先來看個將每個象限平面分割為9的水晶球:

看似複雜的水晶球,其實只要有一個規則可以輕易的求出每一個頂點,我們先使用一個圓球,然後用XY平面的橫剖面說明,在XY象限的90度中 若只有一個平面,則訂N為1,每個象限依此處理,此時可以定出四個頂點,然後將這四個頂點以旋轉體來處理,從XZ象限來訂出旋轉角度,N等於1時必須 以90度旋轉四次,使用此方法所畫出的是一個八面體,如下所示:
N = 1,XY象限切割出 1 個平面,當作旋轉體,每次旋轉 90 度。
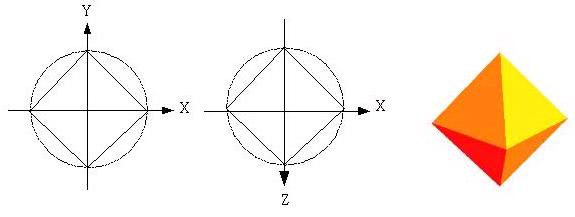
當橫剖面的XY象限分為兩個平面,則N等於2,每個象限依此處理,而旋轉時以45度旋轉八次,則可以畫出如下的圖形:
N = 2,XY象限切割出 2 個平面,當作旋轉體,每次旋轉 45 度。
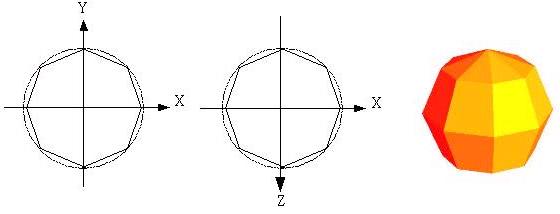
當橫剖面於各個象限的平面分割數越多,也就是N越大時,所畫出的圖形會越接近圓形,例如以下是從N等於3至N等於5的幾個圖形:

您可以數數看,一開始所顯示的水晶球是不是在90度的範圍內有9個平面?!

