二維海龜繪圖法

海龜繪圖法取名海龜並不是因為它的速度像烏龜，而是它繪圖的方式就像海龜前進的方式。

考慮海龜只能前進的情況（我也不知道海龜能不能倒著游？），在2D的情況下，也就是海龜只在一個XY平面運動的情況下，海龜的運動基本上只有前進與轉彎兩個動作，由此開始聯想，定出海龜繪圖法的幾個基本方法：

設定海龜起始位置

也就是將海龜直接放至某個(x, y)座標，而不進行任何的繪製動作。

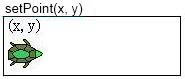
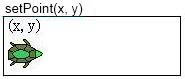
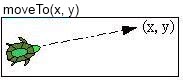
海龜由目前位置游至指定座標

由目前位置游至(x, y)位置，並在經過的路徑畫上直線。

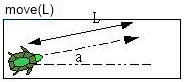
海龜由目前位置游動L長度

無論海龜目前的頭朝向哪一個角度，由目前位置與角度游動L長度，並在經過的路徑上畫上直線。

設定海龜目前頭朝向的角度

角度的計算是以正X軸及頭所成的角度來計算。

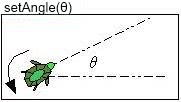
旋轉海龜的頭為指定的角度θ

即目前已成的角度 a 再加上θ，也就是與正X軸最後會成a+θ。

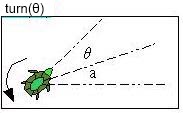
有了以上幾個基本方法，就可以進行各種圖案的繪圖，或是直接擴充海龜繪圖的方法，例如若要在目前的位置上繪製出一個正三角型，由海龜游動的方式，可以如下繪製圖形：

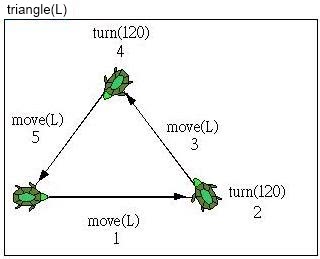
如果要繪製實心的三角形，在撰寫方法時，在海龜游動的同時，記下三個頂點的座標，再呼叫API所提供的繪製實心多邊形方法即可。

如果要繪製點，可以如下結合兩個基本的海龜繪圖方法：

依照以下的描述，您可以自由撰寫並擴充您的海龜繪圖法，使繪圖的功能更加豐富，下面這個Java程式改寫自 Java 於演算法與資料結構之應用，在這邊僅提供程式碼作為參考，解說部份請徑自參考原書：

Turtle.java

package cc.openhome;

import java.awt.*;

public class Turtle {
    public double angle;  // current angle
    public double currentX, currentY;   // current position
    private double wx1, wy1, wx2, wy2; // canvas coordination
    private double vx1, vy1, vx2, vy2; // viewable area
    private double factX, factY;      // scale
    private Graphics g;

    public void setGraphics(Graphics g) {
        this.g = g;
    }

    public Graphics getGraphics() {
        return g;
    }

    public double getCurrentX() {
        return currentX;
    }

    public double getCurrentY() {
        return currentY;
    }

    public void window(double x1, double y1, double x2, double y2) {
        wx1 = x1;
        wy1 = y1;
        wx2 = x2;
        wy2 = y2;
        factX = (vx2 - vx1) / (wx2 - wx1);
        factY = (vy2 - vy1) / (wy2 - wy1);
    }

    public void view(double x1, double y1, double x2, double y2) {
        g.setClip((int) x1, (int) y1, (int) (x2 - x1), (int) (y2 - y1));
        vx1 = x1;
        vy1 = y1;
        vx2 = x2;
        vy2 = y2;
        factX = (vx2 - vx1) / (wx2 - wx1);
        factY = (vy2 - vy1) / (wy2 - wy1);
    }

    public void warp(double l) {
        setPoint(currentX + l * Math.cos(Math.toRadians(angle)), 
                 currentY + l * Math.sin(Math.toRadians(angle)));
    }

    public void move(double l) {
        double x = currentX + l * Math.cos(Math.toRadians(angle));
        double y = currentY + l * Math.sin(Math.toRadians(angle));
        double x1 = (currentX - wx1) * factX + vx1;
        double y1 = (wy2 - currentY) * factY + vy1;
        double x2 = (x - wx1) * factX + vx1;
        double y2 = (wy2 - y) * factY + vy1;
        g.drawLine((int) x1, (int) y1, (int) x2, (int) y2);
        setPoint(x, y);
    }

    public void moveTo(double x, double y) {
        double x1 = (currentX - wx1) * factX + vx1;
        double y1 = (wy2 - currentY) * factY + vy1;
        double x2 = (x - wx1) * factX + vx1;
        double y2 = (wy2 - y) * factY + vy1;
        g.drawLine((int) x1, (int) y1, (int) x2, (int) y2);
        setPoint(x, y);
    }

    public void setPoint(double x, double y) {
        currentX = x;
        currentY = y;
    }

    public void pset(double x, double y) {
        setPoint(x, y);
        moveTo(x, y);
    }

    public void line(double x1, double y1, double x2, double y2) {
        setPoint(x1, y1);
        moveTo(x2, y2);
    }

    public void turn(double a) {
        angle = angle + a;
        angle = angle % 360;
    }

    public void setAngle(double angle) {
        this.angle = angle;
    }
}

以下是使用HTML 5 Canvas時的JavaScript實作：

turtle.js

function Turtle(context) {
    function toRadians(angle) {
        return angle * Math.PI / 180;
    }
    
    function drawLine(x1, y1, x2, y2) {
        context.beginPath();
        context.moveTo(x1, y1);
        context.lineTo(x2, y2);
        context.stroke();
    }
    
    this.angle                               // current angle
        = this.currentX = this.currentY = 0; // current position
        
    var wx1 = wy1 = wx2 = wy2                // canvas coordination
        = vx1 = vy1 = vx2 = vy2              // viewable area
        = factX = factY = 0;                 // scale 
        
    this.context = context;
    
    this.window = function(x1, y1, x2, y2) {
        wx1 = x1;
        wy1 = y1;
        wx2 = x2;
        wy2 = y2;
        factX = (vx2 - vx1) / (wx2 - wx1);
        factY = (vy2 - vy1) / (wy2 - wy1);    
    };
    
    this.view = function(x1, y1, x2, y2) {
        this.context.beginPath();
        this.context.rect(x1, y1, x2 - x1, y2 - y1);
        this.context.clip();
        this.context.stroke();
        this.context.closePath();
        vx1 = x1;
        vy1 = y1;
        vx2 = x2;
        vy2 = y2;
        factX = (vx2 - vx1) / (wx2 - wx1);
        factY = (vy2 - vy1) / (wy2 - wy1);
    };
    
    this.setPoint = function(x, y) {
        this.currentX = x;
        this.currentY = y;
    };
    
    this.setAngle = function(a) {
        this.angle = a;
    };
    
    this.warp = function(l) {
        this.setPoint(this.currentX + l * Math.cos(toRadians(this.angle)),
                      this.currentY + l * Math.sin(toRadians(this.angle)));
    };
    
    this.move = function(l) {
        var x = this.currentX + l * Math.cos(toRadians(this.angle));
        var y = this.currentY + l * Math.sin(toRadians(this.angle));
        var x1 = (this.currentX - wx1) * factX + vx1;
        var y1 = (wy2 - this.currentY) * factY + vy1;
        var x2 = (x - wx1) * factX + vx1;
        var y2 = (wy2 - y) * factY + vy1;
        drawLine(x1, y1, x2, y2);
        this.setPoint(x, y);
    };
    
    this.moveTo = function(x, y) {
        var x1 = (this.currentX - wx1) * factX + vx1;
        var y1 = (wy2 - this.currentY) * factY + vy1;
        var x2 = (x - wx1) * factX + vx1;
        var y2 = (wy2 - y) * factY + vy1;
        drawLine(x1, y1, x2, y2);
        this.setPoint(x, y);  
    };
    
    this.pset = function(x, y) {
        drawLine(x, y, x + 1, y + 1);
    };
    
    this.line = function(x1, y1, x2, y2) {
        this.setPoint(x1, y1);
        this.moveTo(x2, y2);
    };
     
    this.turn = function(a) {
        this.angle = this.angle + a;
        this.angle = this.angle % 360;
    };
}