四元數(Quaternions)為數學家Hamilton於1843年所創造的,您可能學過的是複數,例如:a + b i 這樣的數,其中i * i = -1,Hamilton創造了三維的複數,其形式為 w + x i + y j + z k,其中i、j、k的關係如下:
i2 = j2 = k2 = -1
i * j = k = -j * i
j * k = i = -k * j
k * i = j = -i * k
i * j = k = -j * i
j * k = i = -k * j
k * i = j = -i * k
假設有兩個四元數:
q1 = w1 + x1 i + y1 j + z1 k
q2 = w2 + x2 i + y2 j + z2 k
q2 = w2 + x2 i + y2 j + z2 k
四元數的加法定義如下:
q1 + q2 = (w1+w2) + (x1+x2) i + (y1+y2) j + (z1+z2) k
四元數的乘法定義如下,利用簡單的分配律就是了:
q1 * q2 =
由於q = w + x i + y j + z k中可以分為純量w與向量x i + y j + z k,所以為了方便表示,將q表示為(S, V),其中S表示純量w,V表示向量x i + y j + z k,所以四元數乘法又可以表示為:(w1*w2 - x1*x2 - y1*y2 - z1*z2) +
(w1*x2 + x1*w2 + y1*z2 - z1*y2) i +
(w1*y2 - x1*z2 + y1*w2 + z1*x2) j +
(w1*z2 + x1*y2 - y1*x2 + z1*w2) k
(w1*x2 + x1*w2 + y1*z2 - z1*y2) i +
(w1*y2 - x1*z2 + y1*w2 + z1*x2) j +
(w1*z2 + x1*y2 - y1*x2 + z1*w2) k
q1 * q2 = (S1 + V1)*(S2 + V2) = S1*S2 - V1.V2 + V1XV2 + S1*V2 + S2*V1
其中V1.V2表示向量內積,V1XV2表示向量外積。
定義四元數q = w + x i + y j +z k 的norm為:
N(q) = |q| = x2 + y2 + z2 + w2
滿足N(q) = 1的四元數集合,稱之為單位四元數(Unit quaternions)。
定義四元數定義四元數q = w + x i + y j +zk的共軛(Conjugate)為:
q* = 定義四元數q = w - x i - y j -z k = [S - V]
定義四元數的倒數為:
1/ q = q* / N(q)
說明了一些數學,您所關心的或許是,四元數與旋轉究竟有何關係,假設有一任意旋轉軸的向量A(Xa, Ya, Za)與一旋轉角度θ,如下圖所示:
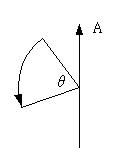
可以將之轉換為四元數:
x = s * Xa
y = s * Ya
z = s * Za
w = cos(θ/2)
s = sin(θ/2)
y = s * Ya
z = s * Za
w = cos(θ/2)
s = sin(θ/2)
所以使用四元數來表示的好處是:我們可以簡單的取出旋轉軸與旋轉角度。
那麼四元數如何表示三維空間的任意軸旋轉?假設有一向量P(X, Y, Z)對著一單位四元數q作旋轉,則將P視為無純量的四元數X i + Y j + Z k,則向量的旋轉經導證如下:
Rot(P) = q p q*
四元數具有純量與向量,為了計算方便,將之以矩陣的方式來表現四元數的乘法,假設將四元數表示如下:
q = [w, x, y, z] = [S, V]
兩個四元數相乘q" = q * q'的矩陣表示法如下所示:
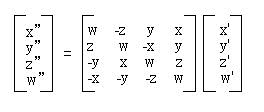
若令q = [S, V] = [cosθ, u*sinθ],其中u為單位向量,而令q'= [S', V']為一四元數,則經過導證,可以得出q * q' * q^(-1)會使得q'繞著u軸旋轉2θ。
由四元數的矩陣乘法與四元數的旋轉,可以導證出上面的旋轉公式可以使用以下的矩陣乘法來達成:
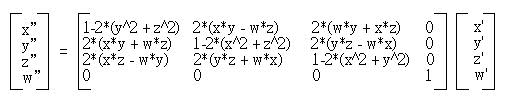
講了這麼多,其實就是要引出上面這個矩陣乘法,也就是說如果您要讓向量(x', y', z')(w'為0)對某個單位向量軸u(x, y, z)旋轉角度2θ,則w = cosθ,代入以上的矩陣乘法,即可得旋轉後的(x", y", z"),如果為了方便,轉換矩陣的最下列與最右行會省略不寫出來,而如下所示:
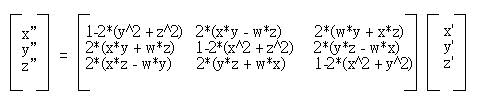
關於四元數與旋轉的更多說明,可以參考 四元數旋轉矩陣,其中也包含了 WebGL 的範例示範。

