平面法線判定法

法線向量判定法適用於無凹陷的凸多面體，例如正多面體或水晶球，其原理為求出每個面的法線向量，如果法線向量的Z 分量大於0（即面朝向我們），則該面為可視，如果法線向量的Z分量小於0，則看不到那個面，則這是個隱藏面，所以無需繪製。

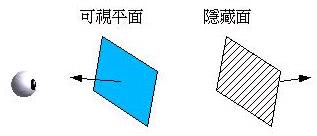
法線向量的選擇是由面上的三個頂點來判定，三個頂點的選擇是依面的逆時針方向的來選出，然後求出這三個頂點所成的兩向量之外積即為法線向量，通常我們取單位法線向量（normalize後的外積），下面這個程式片段可以作為外積計算的參考：

/* Java */
// 取得外積
public static Point op(Point p0, Point p1, Point p2) {
    p1.x = p1.x - p0.x;
    p1.y = p1.y - p0.y;
    p1.z = p1.z - p0.z;

    p2.x = p2.x - p0.x;
    p2.y = p2.y - p0.y;
    p2.z = p2.z - p0.z;

    double x = p1.y * p2.z - p1.z * p2.y;
    double y = p1.z * p2.x - p1.x * p2.z;
    double z = p1.x * p2.y - p1.y * p2.x;

    return new Point(x, y, z);
}

// 計算單位向量
public static Point ev(Point p) {
    double d = Math.sqrt(p.x * p.x + p.y * p.y + p.z * p.z);

    if(d > 0.0) {
        return new Point(p.x / d, p.y / d, p.z / d);
    }

    return p;
}

// 取得nomalize後的外積
public static Point nop(Point p0, Point p1, Point p2) {
    return ev(op(p0, p1, p2));
}

/* JavaScript */
// 取得外積
function op(p0, p1, p2) {
    p1.x = p1.x - p0.x;
    p1.y = p1.y - p0.y;
    p1.z = p1.z - p0.z;

    p2.x = p2.x - p0.x;
    p2.y = p2.y - p0.y;
    p2.z = p2.z - p0.z;

    var x = p1.y * p2.z - p1.z * p2.y;
    var y = p1.z * p2.x - p1.x * p2.z;
    var z = p1.x * p2.y - p1.y * p2.x;

    return new Point(x, y, z);
}

// 計算單位向量
function ev(p) {
    var d = Math.sqrt(p.x * p.x + p.y * p.y + p.z * p.z);

    if(d > 0.0) {
        return new Point(p.x / d, p.y / d, p.z / d);
    }

    return p;
}

// 取得nomalize後的外積
function nop(p0, p1, p2) {
    return ev(op(p0, p1, p2));
}

配合外積，可以利用下面這個程式片段進行隱藏面的判斷與非隱藏面的繪製，其中vet[]是頂點陣列，NFC表示凸面體的平面數量，NVT表示一個平面上的頂點數，ord[][]表示頂點索引陣列：

/* Java */
int N = 0;
Point[][] pvt = new Point[NFC][NVT];
int[] n = new int[NVT];
Point np;

for(int i = 0; i < NFC; i++) {
    for(int j = 0; j < NVT; j++) {
        // 取同一個平面的頂點
        n[j] = ord[i][j];
    }
    // 計算nomalize後的外積
    np = nop(vet[n[0]], vet[n[1]], vet[n[2]]);

    // 如果非隱藏面
    if(np.z > 0) {
        // 儲存頂點
        pvt[N][j] = new Point(vet[n[j]].x, vet[n[j]].y);
        // 可繪製的面+1
        N++;
    }
}

// 畫實心多邊形
for(int i = 0; i < N; i++) {
    fillPolygon(pvt[i], NVT); // 繪製填充多邊型，配合繪圖程式庫
}

/* JavaScript */
var N = 0;
var pvt = [];
for(var i = 0; i < NFC, i++) {
    pvt[i] = [];
}
var n = [];
var np;

for(var i = 0; i < NFC; i++) {
    for(var j = 0; j < NVT; j++) {
        // 取同一個平面的頂點
        n[j] = ord[i][j];
    }

    // 計算nomalize後的外積
    np = nop(vet[n[0]], vet[n[1]], vet[n[2]]);

    // 如果非隱藏面
    if(np.z > 0) {
        // 儲存頂點
        pvt[N][j] = new Point(vet[n[j]].x, vet[n[j]].y);
        // 可繪製的面+1
        N++;
    }
}

// 畫實心多邊形
for(var i = 0; i < N; i++) {
    fillPolygon(pvt[i], NVT); // 繪製填充多邊型，配合繪圖程式庫
}

上面這個程式只是個演算的參考，實作時得依您所使用的語言與API作調整。