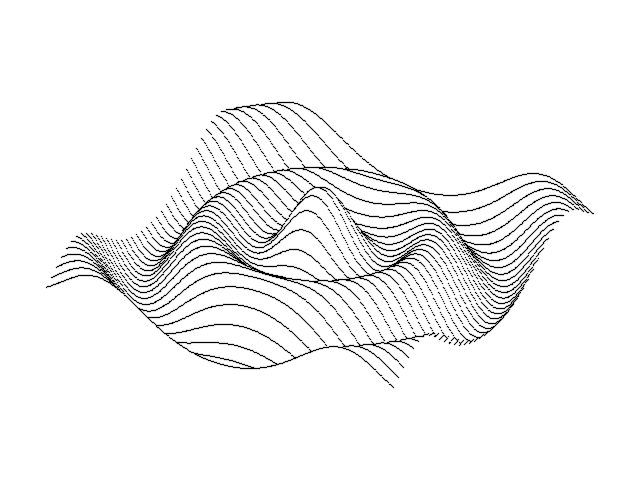
在 函式圖形繪製 的範例中,發現到有一些座標點必須是被遮蓋住,而不應被繪製出來的。
在處理隱藏面的問題時,必須根據繪製圖形來決定不同的方法,對於單純的座標點繪製,可以使用簡單的最大最小法來讓被遮蓋的座標點不被繪製。
最大最小法的原理很簡單,繪製時必須從最接近我們的點開始繪製,也就是由最大的Z座標點開始繪製;最大最小點是根據Y座標的值來決定哪些點應該被繪製,假設繪製圖形時是使用以下的迴圈:
for(z = 200; z >= -200; z-=10) {
for(x = -200; x <= 200; x++) {
//計算座標並繪點
....
}
}
for(x = -200; x <= 200; x++) {
//計算座標並繪點
....
}
}
假設前三次繪圖在Y的坡度上是漸增的,如下所示:
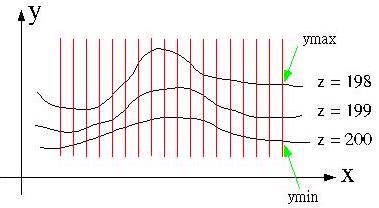
必須記錄每一個x位置上的ymax與ymin,如果在第四次繪製時某些位置上的Y坡度是下降的,則那些位置上的Y必然是位於ymax與ymin之間,此時這些點可以不繪製,如下圖所示:
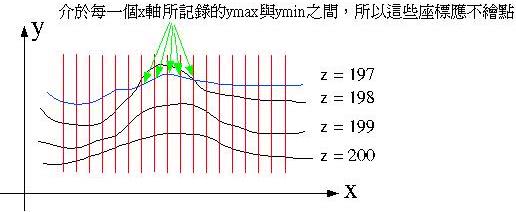
記得在一開始必須將ymax設定為最小的Y值,ymin設定為最大的Y值;以下是將函式繪圖中的範例應用最大最小法繪製的方法與結果:
- Demo.java
package cc.openhome;
import java.awt.Color;
import java.awt.Graphics;
import javax.swing.JApplet;
import static java.lang.Math.*;
public class Demo extends JApplet {
private int orgX;
private int orgY;
private int[] ymax;
private int[] ymin;
public void init() {
super.init();
setBackground(Color.black);
setSize(640, 480);
orgX = getWidth() / 2;
orgY = getHeight() / 2;
ymax = new int[600];
ymin = new int[600];
}
public void paint(Graphics g) {
g.setColor(Color.yellow);
// 重置最大最小點
for(int i = 0; i < ymax.length; i++) {
ymax[i] = 0;
ymin[i] = ymax.length;
}
// 從斜角繪製
// 繞 x 軸轉 30 度,繞 y 軸轉 -30 度
double rotateX = toRadians(30);
double rotateY = toRadians(-30);
double sinRotateX = sin(rotateX);
double cosRotateX = cos(rotateX);
double sinRotateY = sin(rotateY);
double cosRotateY = cos(rotateY);
for(int z = 200; z >= -200; z-=10) {
for(int x = -200; x <= 200; x++) {
double y = 30*(cos(toRadians(sqrt(x * x + z * z)))
+ cos(toRadians(3 * sqrt(x * x + z * z))));
// 立體旋轉,從斜角繪製,調整繪圖中心至視窗中心
int pointX = (int) (orgX + x * cosRotateY + z * sinRotateY);
int pointY = (int) (orgY - (y * cosRotateX -
(-x * sinRotateY + z * cosRotateY) * sinRotateX));
// 最大最小法
if(pointY < ymin[pointX]) {
ymin[pointX] = pointY;
g.drawLine(pointX, pointY, pointX, pointY);
} else if(pointY > ymax[pointX]) {
ymax[pointX] = pointY;
g.drawLine(pointX, pointY, pointX, pointY);
}
}
}
}
}以下是使用HTML5 Canvas的方式(如果瀏覽器支援HTML5 Canvas,例如最新版的Firexfox、Chrome、IE9等,可以直接將下面的內容存為HTML或按下檔名連結,直接載入瀏覽器執行觀看結果:
<!DOCTYPE html>
<html>
<head>
<meta content="text/html; charset=Big5" http-equiv="content-type">
<script type="text/javascript">
window.onload = function() {
function toRadians(angle) {
return angle * Math.PI / 180;
}
var sin = Math.sin;
var cos = Math.cos;
var sqrt = Math.sqrt;
var ymax = new Array(600);
var ymin = [];
for(var i = 0; i < ymax.length; i++) {
// ymax[i] = 0;
ymin[i] = ymax.length;
}
var canvas1 = document.getElementById('canvas1');
var context = canvas1.getContext('2d');
var orgX = canvas1.width / 2;
var orgY = canvas1.height / 2;
var rotateX = toRadians(30);
var rotateY = toRadians(-30);
var sinRotateX = Math.sin(rotateX);
var cosRotateX = Math.cos(rotateX);
var sinRotateY = Math.sin(rotateY);
var cosRotateY = Math.cos(rotateY);
context.beginPath();
for(var z = 200; z >= -200; z-=10) {
for(var x = -200; x <= 200; x++) {
var y = 30*(cos(toRadians(sqrt(x * x + z * z)))
+ cos(toRadians(3 * sqrt(x * x + z * z))));
// 立體旋轉,從斜角繪製,調整繪圖中心至視窗中心
var pointX = parseInt(
orgX + x * cosRotateY + z * sinRotateY);
var pointY = parseInt(orgY - (y * cosRotateX -
(-x * sinRotateY + z * cosRotateY) * sinRotateX));
// 最大最小法
if(pointY < ymin[pointX]) {
ymin[pointX] = pointY;
context.moveTo(pointX, pointY);
context.lineTo(pointX + 1, pointY + 1);
} else if(pointY > ymax[pointX]) {
ymax[pointX] = pointY;
context.moveTo(pointX, pointY);
context.lineTo(pointX + 1, pointY + 1);
}
}
}
context.stroke();
context.closePath();
};
</script>
</head>
<body>
<canvas id="canvas1" width="640" height="480"></canvas>
</body>
</html>
在Firefox中的結果如下: