如果我們要繪製的圖形很多時,在動畫製作時,如果直接畫在前景上,可能會發生圖形一個一個顯現出來的畫面,讓整個畫面不完整呈現。
這時候可使用雙緩衝區(double-buffer)的方法,要準備兩個繪圖物件,其中一個是前景區,也就是您所看到的畫面,另一個繪圖物件您看不到,在 畫面準備好之前,所有的圖形先繪製在您看不到的畫面,當所有的圖形都繪製完畢,再將所有的圖形繪製到前景,此時前景會整個被後繪圖區所覆蓋,完成一次畫面 的播放,下圖為簡單的示意圖:
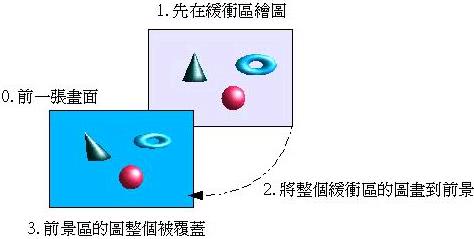
實作雙緩衝區的方法依所使用的API而有所不同,在Java中可以用Image物件來完成,而在使用DirectDraw時,可以使用 Surface來建立,下面這個程式是使用Java來製作,這個程式是至今所有文件內容驗收,包括了頂點配置、索引陣列、動畫、雙緩衝區等等,您可以先觀 看結果:一個繞Y軸旋轉的空心立方塊。
- DoubleBuffer.java
package cc.openhome;
import javax.swing.JApplet;
import java.awt.*;
// 立方體類別
class Point {
public final double x, y, z;
public Point(double x, double y, double z) {
this.x = x;
this.y = y;
this.z = z;
}
}
class Cubic {
public final static int NFC = 6; // 平面數量
public final static int NVT = 8; // 頂點的數量
public final static int NVT_F = 4; // 1個平面的頂點數
public Point[] vt; // 頂點的座標
public int[][] ord; // 頂點索引
public Cubic(int r) {
vt = new Point[NVT];
double sq3 = Math.sqrt(3.0);
vt[0] = new Point(r / sq3, r / sq3, r / sq3);
vt[1] = new Point(r / sq3, r / sq3, -r / sq3);
vt[2] = new Point(-r / sq3, r / sq3, -r / sq3);
vt[3] = new Point(-r / sq3, r / sq3, r / sq3);
for (int i = 0; i < NVT / 2; i++) {
vt[NVT / 2 + i] = new Point(-vt[i].x, -vt[i].y, -vt[i].z);
}
int[][] initOrd = {{0, 1, 2, 3}, {0, 3, 5, 6}, {0, 6, 7, 1},
{4, 7, 6, 5}, {4, 2, 1, 7}, {4, 5, 3, 2}};
ord = new int[NFC][NVT_F];
for (int i = 0; i < NFC; i++) {
for (int j = 0; j < NVT_F; j++) {
ord[i][j] = initOrd[i][j];
}
}
}
}
public class DoubleBuffer extends JApplet implements Runnable {
private Image offScreen;
private Graphics gOffScreen;
private int orgX, orgY;
private Cubic cubic = new Cubic(100);
public void init() {
setBackground(Color.black);
orgX = getWidth() / 2;
orgY = getHeight() / 2;
offScreen = createImage(getWidth(), getHeight());
gOffScreen = offScreen.getGraphics();
gOffScreen.setColor(Color.yellow);
}
public void start() {
(new Thread(this)).start();
}
public void run() {
// 旋轉以斜角繪製圖形
double sinAx = Math.sin(Math.toRadians(30));
double cosAx = Math.cos(Math.toRadians(30));
double[] cosAys = new double[360];
double[] sinAys = new double[360];
for (int i = 0; i < 360; i++) {
cosAys[i] = Math.cos(Math.toRadians(i));
sinAys[i] = Math.sin(Math.toRadians(i));
}
int angle = 330;
double sinAy = sinAys[angle];
double cosAy = cosAys[angle];
Point[] tp = new Point[4];
int[] px = new int[4];
int[] py = new int[4];
// 動畫迴圈
while (true) {
gOffScreen.clearRect(0, 0, getWidth(), getHeight());
for (int i = 0; i < Cubic.NFC; i++) {
for (int j = 0; j < Cubic.NVT_F; j++) {
// 利用索引array取出正確的頂點
tp[j] = cubic.vt[cubic.ord[i][j]];
// 旋轉以斜角繪製圖形
px[j] = (int) (tp[j].x * cosAy + tp[j].z * sinAy);
py[j] = (int) (tp[j].y * cosAx -
(-tp[j].x * sinAy + tp[j].z * cosAy) * sinAx);
px[j] = px[j] + orgX;
py[j] = -py[j] + orgY;
}
// 在緩衝區上縮圖
gOffScreen.drawPolyline(px, py, 4);
}
repaint(); // 重繪畫面
// 暫停 20 毫秒
try {
Thread.sleep(20);
} catch (InterruptedException e) {
e.printStackTrace();
}
// 繞 y 軸轉動
angle = (angle + 1) % 360;
sinAy = sinAys[angle];
cosAy = cosAys[angle];
}
}
// 重新定義update()
public void update(Graphics g) {
paint(g);
}
public void paint(Graphics g) {
// 將緩衝區畫面繪到前景
g.drawImage(offScreen, 0, 0, this);
}
}如果是HTML 5 Canvas的話,視所使用的API而定,可以有各種方式來實現雙緩衝區效果。例如,可以用兩個Canvas互換來達到雙緩衝區的效果。
以下是使用HTML5 Canvas的方式(如果瀏覽器支援HTML5 Canvas,例如最新版的Firexfox、Chrome、IE9等,可以直接將下面的內容存為HTML或按下檔名連結,直接載入瀏覽器執行觀看結果:
<!DOCTYPE html>
<html>
<head>
<meta content="text/html; charset=Big5" http-equiv="content-type">
<script type="text/javascript">
window.onload = function() {
function toRadians(angle) {
return angle * Math.PI / 180;
}
var sin = Math.sin;
var cos = Math.cos;
var sqrt = Math.sqrt;
function Point(x, y, z) {
this.x = x;
this.y = y;
this.z = z;
}
var V_INDEX = [
[0, 1, 2, 3], [0, 7, 6, 1], [4, 5, 6, 7],
[2, 5, 4, 3], [0, 3, 4, 7], [1, 6, 5, 2]
];
var L = 100;
var VETEX = [
new Point(L, L, L), new Point(L, -L, L),
new Point(L, -L, -L), new Point(L, L, -L),
new Point(-L, L, -L), new Point(-L, -L, -L),
new Point(-L, -L, L), new Point(-L, L, L)
];
// 旋轉以斜角繪製圖形
var ax = toRadians(30);
var ay = toRadians(30);
var sinAx = sin(ax);
var cosAx = cos(ax);
//var sinAy = sin(ay);
//var cosAy = cos(ay);
var cosAys = [];
var sinAys = [];
for(var i = 0; i < 360; i++) {
cosAys[i] = cos(toRadians(i));
sinAys[i] = sin(toRadians(i));
}
var angle = 330;
var sinAy = sinAys[angle];
var cosAy = cosAys[angle];
var px = [];
var py = [];
var canvas1 = document.getElementById('canvas1');
var canvas2 = document.getElementById('canvas2');
var orgX = canvas1.width / 2;
var orgY = canvas1.height / 2;
var context1 = canvas1.getContext('2d');
var context2 = canvas2.getContext('2d');
// 先繪製背景
var context = context2;
setTimeout(function() {
context.beginPath();
for(var i = 0; i < 6; i++) {
for (var j = 0; j < 4; j++) {
// 利用索引陣列取出正確的頂點
var v = VETEX[V_INDEX[i][j]];
// 旋轉以斜角繪製圖形
px[j] = parseInt(
v.x * cosAy + v.z * sinAy + orgX);
py[j] = parseInt(v.y * cosAx -
(-v.x * sinAy + v.z * cosAy) * sinAx + orgY);
}
context.moveTo(px[0], py[0]);
for(var k = 1; k < 4; k++) {
context.lineTo(px[k], py[k]);
}
}
context.clearRect(0, 0, canvas1.width, canvas1.height);
context.stroke();
// 置換Canvas與Context
if(context === context2) {
document.body.replaceChild(canvas1, canvas2);
context = context1;
}
else {
document.body.replaceChild(canvas2, canvas1);
context = context2;
}
// 繞 y 軸轉動
angle = (angle + 1) % 360;
sinAy = sinAys[angle];
cosAy = cosAys[angle];
setTimeout(arguments.callee, 20);
}, 20);
};
</script>
</head>
<body>
<canvas id="canvas1" width="640" height="480"></canvas>
<canvas id="canvas2" width="640" height="480"></canvas>
</body>
</html>
