Java 開發者的函數式程式設計（2）代數資料型態

English

我們大多熟悉物件導向程式設計，熟悉抽象資料型態（Abstract data type, ADT）。抽象資料型態的模型中封裝了資料結構與實作，僅透露互動時的公開介面；然而，代數資料型態（Algebraic data type）相對地曝露了基本的資料結構及規律性，在函數式程式設計的領域中，代數資料型態是基本元素。
（ADT 廣泛應用為 Abstract Data Type 的縮寫，在函數式程式設計中並不使用這個縮寫，因此英文中都直接使用 Abstract Data Type 作為全名。）
Java 是物件導向程式語言，對代數資料型態沒有直接的支援，有兩種方式可以模擬該型態。由於代數資料型態會曝露基本的資料結構，因而可使用具公開值域（Field）的類別來模擬代數資料型態，不過，許多物件導向原則並不鼓勵公開值域，如此一來就得尋找其他方式來模擬。因為代數資料型態會曝露規律性，規律性這聽起來像個行為表現，在 Java 中討論行為時，通常會使用 interface 加以定義。
以清單類型為例，我們知道 Java SE API 中定義了 java.util.List，而這個 List 是抽象資料型態。如果想要以代數資料型態的模型來定義清單該怎麼做？在函數式程式設計中，清單會是由首（head）元素與尾（tail）清單組成。若想使用 interface 來定義（或模擬）這樣的清單則會是：

public interface List<T> {
    T head();
    List<T> tail();
}

這種清單的實例之一是空清單，若運用以上介面來實作一個空清單的話，可以如下…

public class AlgebraicType {
    private static List<? extends Object> Nil = new List<Object>() {
        public Object head() {
            return null;
        }
        public List<Object> tail() {
            return null;
        }
        public String toString() {
            return "[]";
        }
    };

    @SuppressWarnings("unchecked")
    public static <T> List<T> nil() {
        return (List<T>) Nil;
    }
}

也就是說，空清單沒頭沒尾。為了方便，我們也定義了一個 static 的 nil 方法來傳回空清單，有了空清單的定義之後，接下來就可以定義具單一元素的清單，為具有首元素及尾清單 Nil 的組合。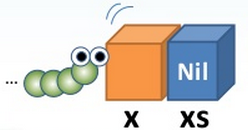

functional-programming-for-java-developers-2-algebraic-data-types-1

如果有個清單 xs，打算在其前頭放個元素 x，新清單就是將 x 當作首元素而 xs 作為尾元素而得來。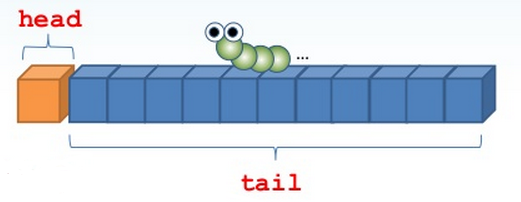

functional-programming-for-java-developers-2-algebraic-data-types-2

為了方便，我們來定義一個 static 的 con 方法，用以建立新清單。

public class AlgebraicType {
    ...
    public static <T> List<T> cons(final T x, final List<T> xs) {
        return new List<T>() {
            private T head;
            private List<T> tail;
            { this.head = x; this.tail = xs; }
            public T head(){ return this.head; }
            public List<T> tail() { return this.tail; }
            public String toString() { return head() + ":" + tail(); }
       };
    }
}

一旦有了 nil 與 con 方法，具有單一元素的清單，就可以使用以下的程式碼來建立：

cons(1, nil()); // 1:[]

具有元素 2、1 的清單，則可以使用以下程式碼來建立：

cons(2, cons(1, nil())); // 2:1:[]

具有元素 3、2、1 的清單，則可以使用以下程式碼來建立：

cons(3, cons(2, cons(1, nil()))); // 3:2:1:[]

為了方便，可以定義一個 list 方法，使用傳入的不定長度引數建立新清單並傳品。

public class AlgebraicType {
    …
    @SafeVarargs
    public static <T> List<T> list(T... elems) {
        if(elems.length == 0) return nil();
        T[] remain = Arrays.copyOfRange(elems, 1, elems.length);
        return cons(elems[0], list(remain));
    }
}

如此要建立具元素 1、2、3、4 的清單就可以如下：

list(1, 2, 3, 4); // 1:2:3:4:[]

這邊定義的 List 是代數資料型態，它易於分解，也就是說，任何清單值都可以用兩種方式來建立，一個可能的值就是空清單 Nil，其它的清單值就僅僅是由首元素與尾清單建構而來，這也就是我一開始談到的，代數資料結構會曝露基本資料結構及規徑性。
那麼，為什麼代數資料型態適用於分而治之（Divide-and-conquer）的場合？以這邊的 list 方法為例，它將問題分解為兩個子問題。一個子問題是，呼叫 list 時不給任何引數，此時，list 方法只會傳回空清單。另一個子問題是，呼叫 list 時給定一個或多個引數，解決方案是，使用第一個引數作為首元素，而剩餘的引數作為尾清單的話，就可以使用 con 來建立包括所有給定引數的清單。
這就又有一個問題了，怎麼用剩餘引數作為尾清單？可以遞迴地用剩餘引數來呼叫 list 方法。正如 Java 開發者的函數式程式設計（1）中提到的，在將問題分解之後，遞迴僅僅也經常是自然的呈現形式，將代數資料型態與遞迴結合，就會成為分解問題時一個非常有用的方式。