Haskell Tutorial（10）從 Tuple 初試模式比對


回顧一下〈Haskell Tutorial（6）從 List 處理初試函數式風格〉、〈Haskell Tutorial（7）filter、map、fold 模式〉，你會發現一個 List 處理遵循著一個模式，取 List 首元素與尾清單，這樣的模式可以定義為一個型態，也就是代數資料型態（Algebraic data type）中的一種，別嚇到了，現在還不是正式介紹代數資料型態的時機，我只是想先談談模式比對（Pattern matching）。

先來看 Tuple

在談模式比對之前，先來看看 Tuple 這個東西會有幫助，跟 List 類似，Tuple 也是個容器，你可以 () 來建立一個 Tuple，例如使用 (1, 2, 3) 建立一個內含數字 1、2、3 的 Tuple，或者是使用 (1, "Justin Lin", 89.1) 建立一個內含 1、"Justin Lin" 與 89.1 的 Tuple，看出來跟 List 哪邊不同了嗎？List 中必須得是同一型態的元素，而 Tuple 中的元素可以有各自不同型態。

有些函式會產生 Tuple，例如說 zip，你可以給它兩個 List，它會將元素兩兩配對，產生一個內含 Tuple 的 List：

zip 函式

如果是成對的 Tuple，可以使用 fst 來取第一個元素，用 snd 來取第二個元素：

fst、snd 函式

如果是超過兩個以上元素的 Tuple 呢？可以用模式比對：

模式比對

如果你使用 :t 來測試，number 會是 Integer、name 是 [Char]，而 score 是 Double，實際上，一個 Tuple 實例也是有型態，只是它沒有名稱：

測試 Tuple 型態

沒辦法使用 (1) 來建立單元素的 Tuple，想想看如果可以，這會是個 (Integer) 型態的 Tuple，那為什麼不直接寫 1 就好！

函式可以接受 Tuple 或傳回 Tuple，因為 Tuple 本身有型態，這會是函式簽署的一部份：

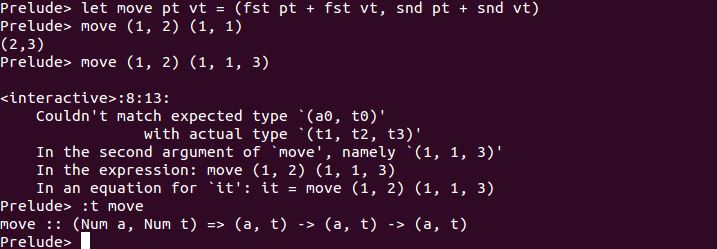
使用 Tuple 作為引數

這從定義 move 是個可以從點 pt 根據指定向量 vt 移動後，傳回新點座標的函式，Haskell 自動推斷出 move 必須是個能接受兩個 Num 行為元素的 Tuple，你傳入 (1, 1, 3) 就會引發錯誤。

模式比對的應用

當你使用 Tuple 來裝填一些元素時，事後你必然會需要取出當中的元素，無論你取得元素之後目的為何，Tuple 比對元素的模式很單純，就是一個蘿蔔一個坑，你可以使用 let (number, name, score) = (1, "Justin", 89.1) 來比對，如果某個坑不需要名稱，那用 _ 空下來就可以了，例如只想取得分數，那可以寫為 let (_, _, score) = (1, "Justin", 89.1)，這樣 score 也會是 89.1。

這不過是模式比對的一種形式，函式上也可以應用模式比對，例如求費式數（Fibonacci number）：

fibonacci :: Int -> Int
fibonacci n =
    if n == 0 || n == 1
        then n
        else fibonacci (n - 1) + fibonacci (n - 2)

這個 fibonacci 實際上就是比對三種情況，0、1 與其他整數，這種可以改為模式比對：

fibonacci :: Int -> Int
fibonacci 0 = 0
fibonacci 1 = 1
fibonacci n = fibonacci (n - 1) + fibonacci (n - 2)

這比使用 if .. else 清楚多了，順便看一下費式數的定義，就會發現可以很容易地對應：

F0 = 0
F1 = 1
Fn = Fn-1 + Fn-2

上頭的 move 函式也可以改為模式比對：

參數上使用模式比對

模式比對可以出現在許多地方，可以使用名稱的地方，基本上就有可能使用模式比對，例如 List comprehension，底下這個範例可以將兩個 List 的元素兩兩相加：

List comprehension 中使用模式比對

Tuple 不是 List

別把 Tuple 當成是可以容納型態各異元素的 List，List 有它自己的模式，不過，這邊作個有趣的範例，讓你使用 Tuple 來模擬 List，並從中瞭解一下模式比對與型態之間的關係。

你需要一個可以容納正整數的清單，假設現在 Haskell 中沒有 List 這東西，因此，你需要自己定義，在研究過你手邊的問題後，你發覺到處理這些問題，基本上都有取清單首元素與尾清單這個動作，因此，你使用 Tuple 來容納首元素與尾清單，也就是 (hd, tl) 來表示一個清單，你需要有個 con 函式，來讓你可以簡單地在一個既有清單前放上一個元素：

con x lt = (x, lt)

這麼一來，如果 () 用來代表空清單，你就可以用 con 來構造清單了 ：

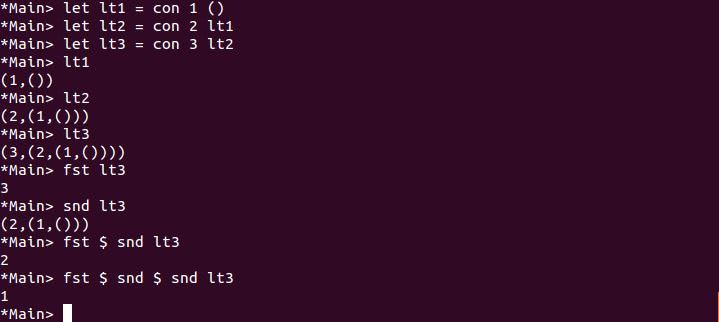
用 Tuple 模彷 List

看起來是蠻像的，fst 感覺就像是 head，而 snd 感覺就好像是 tail，而 con 就類似 : 了，這可以用來突顯出，Tuple 終究不是 List，你也許會想嘗試用這邊的模擬，以及 fst、snd 的概念，來試著實作出〈Haskell Tutorial（7）filter、map、fold 模式〉中的 filter'、map' 等函式，可惜的是，這終究只是模擬，因為 Tuple 實際上有型態，因此，你的 con 實際上會不斷產生新的型態，也因此，你無法具體地在遞迴時設定終止條件，因為遞迴時接受的引數型態必須是一致的。

初探代數資料型態

上面的模擬帶出了一個需求：你需要為 List 定義專用的型態，而不是臨時使用 Tuple 來建立一個匿名的型態。在 List 定義的專用型態中，空清單是個 List，或者是使用 con 從既有的元素及 List 中來構造新的 List。使用 Haskell 的代數資料型態定義語法的話：

data List a = Empty | Con a (List a) deriving (Show, Read, Eq, Ord)

這當中有許多細節，現在將重點先擺在 Empty | Cons a (List a)，這自定義的 List 型態，Empty 代表空清單，而 Con a (List a) 表示可使用 Con 從既有的元素及 List 中來構造新的 List，這就是代數資料型態的特色之一，函式也會是型態定義的一部份。

現在，我們可以像剛剛一樣，使用 Con 來構造清單了，而且，你可以依代數資料型態的定義來進行模式比對：

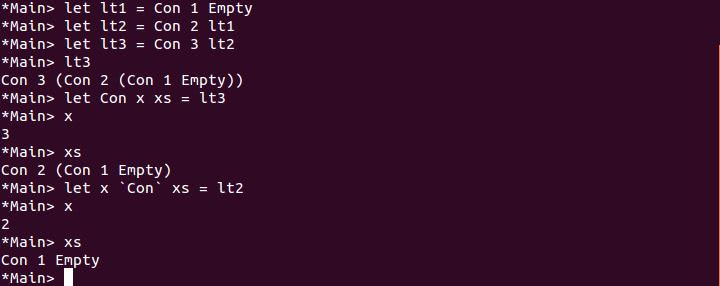
List 與模式比對

很酷不是嗎？實際上，你不用自己定義 List，因為 Haskell 中就有，[] 就相當於上頭 Empty 的角色，而 : 就相當於 Con 的角色，來作個對比吧！

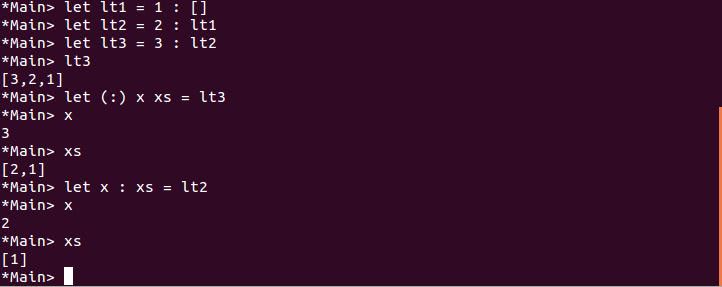
List 與模式比對

之後有機會，會正式介紹代數資料型態的語法，至於現在，你應該知道，為什麼 List 可以使用模式比對拆解其中元素了，而又為什麼，你不能用 xs ++ ys 這樣的模式比對了，因為 List 型態本身就不是這樣定義的。

因此，對於〈Haskell Tutorial（7）filter、map、fold 模式〉中的這個 filter' 函式：

filter' :: (Int -> Bool) -> [Int] -> [Int]
filter' cond lt =
    if null lt then lt
    else
        if cond $ head lt then head lt : (filter' cond $ tail lt)
        else filter' cond $ tail lt

可以直接改寫為：

filter' :: (Int -> Bool) -> [Int] -> [Int]
filter' _ [] = []
filter' cond (x:xs) =
    if cond x then x : filter' cond xs
    else filter' cond xs

看起來簡潔多了吧！其中 filter' _ [] 中的 _ 是因為，我們不需要到傳進來的引數，因此就不用給名稱了。如果你知道 [1, 2, 3, 4] 其實是 1:2:3:4:[] 的語法蜜糖，那麼，就可以自由地設定你想要的模式：

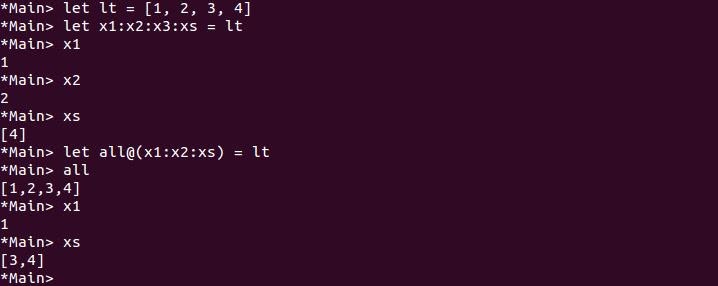
List 與模式比對

最後一個 all@(x1:x2:xs) 模式，除了各拆解資料至 x1、x2 與 xs 之外，亦令 all 為原有的整體資料。

接下來還是給點功課吧！你可以試試看，將〈Haskell Tutorial（6）從 List 處理初試函數式風格〉、〈Haskell Tutorial（7）filter、map、fold 模式〉有用到 head、tail 的函式，改用模式比對來處理！