如果你是初學 Haskell,且能一路看到這篇文章,應該算是步入 Haskell,或說是步入了函數式程式設計的大門了,而這也是我寫 Haskell Tutorial 的目的,往後還有更多的東西等著發掘,為此,我這邊以〈發掘更具組合性的抽象〉為題,作為 Haskell Tutorial 的結束。
加總樹的節點值
記得〈Haskell Tutorial(19)Data.Set 與 Data.Map 模組〉中,最後的題目是希望你實作出一個 Tree 型態嗎?我是這麼實作的:
data Tree a = EmptyTree | Node a (Tree a) (Tree a)
singleNode :: a -> Tree a
singleNode x = Node x EmptyTree EmptyTree
insert :: (Ord a) => a -> Tree a -> Tree a
insert x EmptyTree = singleNode x
insert x (Node a l r)
| x == a = Node x l r
| x < a = Node a (insert x l) r
| x > a = Node a l (insert x r)
fromList :: Ord a => [a] -> Tree a
fromList [] = EmptyTree
fromList (x:xs) = insert x $ fromList xs
node :: (Ord a) => a -> Tree a -> Bool
node x EmptyTree = False
node x (Node a l r)
| x == a = True
| x < a = node x l
| x > a = node x r
toList :: Tree a -> [a]
toList EmptyTree = []
toList tree = con [] tree
where
con lt EmptyTree = lt
con lt (Node a l r) = con r (a : (con l lt))
instance Show a => Show (Tree a) where
show tree = "fromList " ++ (show . toList) tree
現在將重點放在 toList 的實作,我做了什麼?我從 [] 開始,在呼叫內部的 con 函式過程中,如果到達了左子樹的葉節點,就折下這個葉節點放到 List 前端(也就是使用 : 函式),左子樹訪問完就談問右子樹,每次也都是折下一個葉節點放到 List 前端。
如果使用動畫來顯示這個過程的話,就可以清楚地看到,就像是在折疊一顆樹:
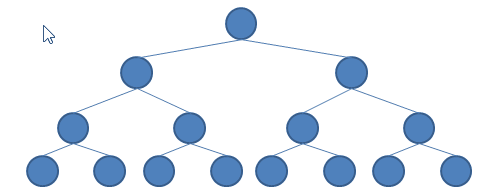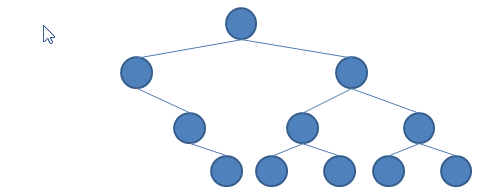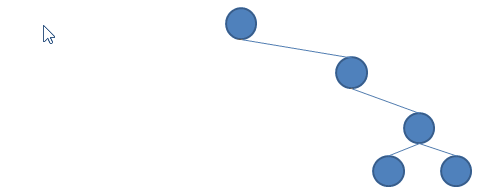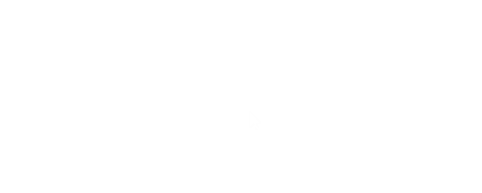
假設現在有一顆樹,節點值都是整數,想將所有節點值加總該怎麼做呢?我們可以使用上頭的 toList 將樹轉為 List,然後再使用 sum 來求得加總,不過,我們自己來寫一個:
sumTree :: Tree Integer -> Integer
sumTree tree = sumIt 0 tree
where
sumIt init EmptyTree = init
sumIt init (Node a l r) = sumIt (a + (sumIt init l)) r
如何?仔細一看,這跟上頭的 toList 根本就是差不多的東西,只是一個用了 :,而另一個用了 +,如果這些函式是被當成引數傳入的話,那我們可以寫個 foldTree:
foldTree :: (a -> b -> a) -> a -> Tree b -> a
foldTree _ z EmptyTree = z
foldTree f z (Node a l r) = foldTree f (f preZ a) r
where preZ = foldTree f z l
那麼,toList 與 sumTree 就可以分別如下使用 foldTree 實作:
toList :: Tree a -> [a]
toList tree = foldTree (\z a -> a : z) [] tree
sumTree :: Tree Integer -> Integer
sumTree tree = foldTree (+) 0 tree
Foldable Typeclass
foldTree 看起來很像可以處理 List 的 foldl(也就是定義在 Data.List 中的 foldl),實際上,如果折疊樹時是從右子樹開始,實作出來的就像是可處理 List 的 foldr 了,看來可以折疊的並不只有 List,對於可折疊的行為,Haskell 在 Data.Foldable 模組中定義了 Foldable 這個 Typeclass。
在 Data.Foldable 模組中也有定義 foldl 等函式,先來看看看它們的型態與使用方式:

相對於只能處理 List 的 foldl :: (a -> b -> a) -> a -> [b] -> a,Data.Foldable 模組中的 foldl 函式,第三個可接受的引數必須具有 Foldable 的行為,最直覺的就是先試試看 List:

想要實現 Foldable,可以實作它的 foldr :: (a -> b -> b) -> b -> t a -> b 或 foldMap :: Monoid m => (a -> m) -> t a -> m,對於 List,實作 Foldable 的 foldr,只要令其等於 Data.List 中的 foldr 函式就可以了,如果想要讓上頭的 Tree 也成為 Foldable,可以如下實作:
import Prelude hiding (foldr)
import Data.Foldable hiding (toList)
...
instance Foldable Tree where
foldr _ z EmptyTree = z
foldr f z (Node a l r) = foldr f (f a preZ) l
where preZ = foldr f z r
這麼一來,我們自定義的 Tree 也可以直接使用 Data.Foldable 模組的 foldr、foldl 等函式了:

Monoid Typeclass
另一個實作 Foldable 的方式,是實作它的 foldMap :: Monoid m => (a -> m) -> t a -> m,不過受到了 Monoid 的限制,這是什麼?你可以先思考一下,如果想要實作一個通用的 foldr 會需要哪些條件?
你能接受的函式必須是二元函式,而且必須具有結合律(Associativity),例如,因為 (1 + 2) + 3 的結果會與 1 + (2 + 3) 相同,因此 + 具有結合律,這是因為事先無法預料可以折疊的資料型態會是什麼樣的結構,被丟進函式處理的兩個值,可能是從結構中任意處取得,如果函式不具備結合律,使用通用的 foldr 結果就可能不正確。
另外,你的函式必須具有恒等值(Identity),函式套用恒等值與某值,結果還會是該值,例如,0 對 + 是個恒等值,因為任何數與 0 相加都會是該數,1 + 0 還是 1、2 + 0 還是 2,類似地,1 對 * 是個恒等值,因為任何數與 1 相乘,結果還是該值,2 * 1 還是 2、3 * 1 還是 3。
這個考量同樣是因為,事先無法預料可以折疊的資料型態會是什麼樣的結構,因此通用的 foldr 首次執行時,必須有個初始的恒等值才能做為開始。
這些行為被 Haskell 定義為 Data.Monoid 中的 Monoid 這個 Typeclass,它要實作的函式有 mempty :: m 與 mappend :: m -> m -> m,來看看 List 怎麼實作 Monoid:
instance Monoid [a] where
mempty = []
mappend = (++)
對於 List 來說,++ 是個具有結合律的函式,因為 ([1, 2] ++ [3, 4]) ++ [5, 6] 結果與 [1, 2] ++ ([3, 4] ++ [5, 6]) 同樣是 [1,2,3,4,5,6],而對於 ++ 來說,[] 就是恒等值,因為 [1, 2] ++ [] 還是 [1, 2],[3, 4] + [] 還是 [3, 4]。
因此,mappend 就是用來實現具有有結合律的二元函式,而 mempty 就是用來設定恒等值了,知道這些之後,就可以知道,為什麼可以使用 F.foldl (++) [] [[1, 2], [3, 4], [5, 6]] 來取得一個 [1, 2, 3, 4, 5, 6] 的結果了。
那麼,該怎麼實作 foldMap?重新來看一下它的型態 Monoid m => (a -> m) -> t a -> m,foldMap 接受一個函式,一個 Foldable 的實例,最後傳回一個值,我們接受的函式之傳回值與 foldMap 的傳回值,都是 Monoid 實例。
對於一個 List,是這樣想的,可以看成是 x:xs,實作 foldMap 時,foldMap f xs 會得到一個 List(一個 Monoid),而 f x 也會得到一個 List(一個 Monoid),結果就是 (f x) ++ (foldMap f xs),也可以寫成 (f x) `mappend` (foldMap f xs)。
在 Haskell 的 Foldable Typeclass 原始碼中,foldr 實作時使用了 foldMap,f 是在 foldr 當中產生並給 foldMap 的;實際上不用管 f 是什麼,只要記得,f 會套用到目前的元素值得到一個 Monoid,而 foldMap 會套用到其他子結構得到其它 Monoid,mappend 再將這些 Monoid 結合起來運算,這就是 foldMap 的實作方式了。
那麼樹的話,就可以看成是 f 套用到目前的節點值得到一個 Monoid,foldMap 套用到左子樹得到一個 Monoid,foldMap 套用到右子樹得到一個 Monoid,然後,你使用 mappend 將這三個 Monoid 結合運算:
instance Foldable Tree where
foldMap f EmptyTree = mempty
foldMap f (Node x l r) =
(foldMap f l) `mappend` (f x) `mappend` (foldMap f r)
簡單來說,如果是 List,想著可以從首元素得到一個 Monoid,尾清單得到一個 Monoid,如果是樹,可以想著從左子樹、節點、右子樹分別得到一個 Monoid,而這些 Monoid 又該如何結合就對了。
繼續前進
真是有趣!如果你直接看 Monoid,大概會摸不著頭緒,為什麼一個恒等值,一個具結合律的二元函式,要合起來定義為一個 Typeclass,然而,如果從折疊資料結構這類的例子來想,試著抽取出共同行為,讓它通用化,就會發現這樣的考量有其道理。
重點是,當這樣的共同行為被抽取出來、通用化之後,就可以將既有的函式等組合進來使用,而不用重新實作類似的行為,就像 List 在實作 Fordable 時,就不要令 Data.List 的 foldr 為 Foldable 就可以了。
這類具有組合性且可抽取的行為還有很多,就如這篇一開始說的,你已經進入了大門,不過,後續還有很多可以探索的!至少,對我來說,還有很多可以玩的呢!

