Haskell Tutorial（28）活用 Applicative 的 pure 與 <*>
Applicative 的 pure 將指定的函式置入與值相同的情境 f，而 <*> 用指定的函式對 Applicative 中的情境 f 中的值進行套用，這個套用的過程被隱藏起來了，因而你只要知道，某函式原本能對 Applicative 中的值做套用，該函式就能用來對 Applicative 做套用。

基本函式的套用

就從頭開始來來看些實際例子吧！在〈Haskell Tutorial（2）一絲不苟的型態系統〉中，我們自定義了第一個函式 doubleMe，基本上可適用任何 Float 引數：

doubleMe :: Float -> Float
doubleMe x = x + x

如果 doubleMe 10 就會是 20，這沒問題，如果有個 Just 10 呢？別急著為它定義新函式，如果知道 Maybe 是個 Applicative，就只要 pure doubleMe <*> Just 10，得到一個 Just 20，如果知道 <$> 的話，那麼寫成 doubleMe <$> Just 10 會更容易閱讀：

這是單參數函式的情況，那麼多參數函式呢？例如定義一個 addThreeNumber：

在〈Haskell Tutorial（6）從 List 處理初試函數式風格〉中第一次談到 : 函式，如果你有個 List 是 [1, 2, 3]，實際上它是 1:2:3:[]，如果你有個 [2, 3]，你可以使用 1:[2, 3] 得到一個 [1, 2, 3]，如果你有個 Just 1 與 Just [2, 3] 呢？

如果你有個 '*' : "Justin"，那就會得到一個 "*Justin"，別老是舉 Maybe 為例好了，如果你有個 IO Char，想要與 getLine 傳回的 IO String 直接使用 : 得到一個 IO String 呢？

部份套用、Lambda與函式合成的情況

既然一個基本的函式可以套用在 Applicative 上，那麼一個函式被部份套用後，傳回一個函式自然也可以套用在 Applicative 上囉！

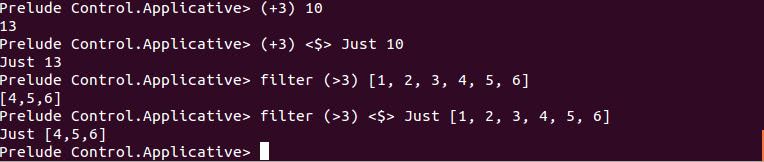
有 Lambda 的情況呢？

那麼，函式合成自然也就沒問題：

函式合成的意思就是，像 (abs . sum) [1, -2, 3, -4]，結果與 abs (sum [1, -2, 3, -4]) 相同，而我們知道，. 不過也只是一個函式，因此，(abs . sum) [1, -2, 3, -4] 也可以寫為 (.) abs sum [1, -2, 3, -4]，也就是說，(.) abs sum [1, -2, 3, -4] 的結果會與 abs (sum [1, -2, 3, -4])，進一步應用在 Applicative 就是：

Applicative 定律

如同 Functor 在實作時，有其應遵守的 Functor 定律，也就是函式在實作時必須得遵守的契約，Applicative 也有其應遵守的規範，這可以在 Control.Applicative 的文件中找到：

• Identity：pure id <*> v = v
• Composition：pure (.) <*> u <*> v <*> w = u <*> (v <*> w)
• Homomorphism：pure f <*> pure x = pure (f x)
• Interchange：u <*> pure y = pure ($ y) <*> u

既然某函式原本能對 Applicative 中的值做套用，該函式就能用來對 Applicative 做套用，那麼從這個角度來思考一個 Applicative 在實作時，應當遵守的 Applicative 定律也就不難理解，就像方才最後的函式合成例子，就是在示範 Maybe Applicative 符合定律中 Composition 的規範。

（Haskell 不會檢查你的實作是否符合 Functor、Applicative 等定律，實作這類規範是開發者的職責，這就像是在 Java 中，實作 equals 必須具備 Reflexive、Symmetric、Transitive、Consistent 等，而實作 hashCode 時也有其規範，而開發者自身應當留意這類規範的實現，另一種說法則是 … 「法律是給守法的人看的」 … XD）