Haskell Tutorial（27）可直接函式套用的 Applicative


如果你有個 Just 10 與一個 Just 5，你可能會希望對它們進行相加，而得到一個 Just 15，當然，直接 (Just 10) + (Just 5) 是行不通的，也許可以定義一個 add 函式來解決這個問題：

add :: Num a => Maybe a -> Maybe a -> Maybe a
add (Just a) (Just b) = Just (a + b)
add Nothing  _        = Nothing
add _        Nothing  = Nothing

如此一來，你就可以使用 add (Just 10) (Just 5) 來達到需求，不過，如果你需要 (Just 10) * (Just 5) 能得到 Just 50 的效果呢？其他像是 List 會不會有這種需求呢？像是希望能 add ["Justin", "Monica", "Irene"] ["Happy", "Lucky", "Healthy"] 而得到 ["JustinHappy", "JustinLucky", "JustinHealthy", "MonicaHappy", "MonicaLucky", "MonicaHealthy", "IreneHappy", "IreneLucky", "IreneHealthy"] 呢？

也就是說，我們希望將 add (Just 10) (Just 5) 這類的操作通用化！

從 Maybe 開始

我們還是從最熟悉的 Maybe 開始，在這之前先思考一下，+、-、*、/ 這類的函式，它們的型態是 Num a => a -> a -> a，也就是接受兩個引數後傳回一個值的函式，不過，從另一個角度來看，因為 Haskell 中的函式可以部份套用，因此你也可以看成是 Num a => a -> (a -> a)，也就是接受一個引數，然後傳回一個函式，也因此，你可以將 (+10)、(-5) 這些函式當作引數，傳給另一個函式。

因此，來思考一下上頭 add 函式，它接受兩個 Maybe a，傳回一個 Maybe a，但是從另一個角度來看，它可以是接受一個 Maybe a，傳回一個 Maybe a -> Maybe a 的函式，要怎樣得到一個 Maybe a -> Maybe a 的函式呢？這感覺像是之前 Functor 介紹中，fmap 會做的事，如果你有一個 Just 5，fmap (+10) (Just 5) 會得到 Just 10，此時 fmap (+10) 就是一個 Maybe Integer -> Maybe Integer 的函式：

Maybe Integer -> Maybe Integer

問題是，我們不能直接寫死 10 這個數字，重新思考！先回憶一下 fmap 的型態 (a -> b) -> f a -> f b，它的第一個參數接受一個 (a -> b) 的函式，那可以傳入 +、-、*、/ 這類的函式嗎？可以！很奇怪嗎？+、-、*、/ 這類的函式，型態不是 a -> a -> a 嗎？是沒錯，但你也可以說它們是 a -> (a -> a)，因此，fmap 是可以接受 +、-、*、/ 這類的函式。

那麼，如果 fmap (+) (Just 10) 的話會如何？10 會與 + 部份套用，得到一個 Just (10 +) 的值，型態是 Maybe (a -> a)，如果可以取出 a -> a 這個函式，假設是 f，繼續使用 fmap f (Just 5)，就可以得到 Just 15，從 Just 10 對應到 Just 5，這不就是我們要的？讓我們將這個過程寫出來：

fmap

如果 + 一開始使用 Just (+) 的話呢？

fmap

這就出現了一個重複的流程，將 Just 中的函式取出，直接當作 fmap 的第一個引數，而 Just something 就是第二個引數，來將這個流程定義為一個函式，並考慮 Nothing 的情況：

op :: Maybe (a -> b) -> Maybe a -> Maybe b
op (Just f) something = fmap f something
op Nothing _ = Nothing

現在有了 op 函式，將 Just 中的函式取出，直接當作 fmap 的第一個引數，而 Just something 就是第二個引數的這個流程就可以重複使用了，因此上頭從 Just (+)、Just 10 到 Just 5 的這個過程，就可以寫為：

fmap

簡單來說，透過 op，你就可以使用 Just (+) 中的 + 函式，來對 Just 10、Just 5 中的 10 與 5 做套用，得到一個 Just 15，願意的話，你也可以使用 ++ 等其他的函式了，例如：

fmap

Maybe Applicative

現在，op 這個函式對 Maybe 夠通用了，它的型態是 Maybe (a -> b) -> Maybe a -> Maybe b，如果 Maybe 這個型態可以參數化的話呢？像是以 [] 為實例？這麼一來，就可以是 f (a -> b) -> f a -> f b，而 Haskell 中 Control.Applicative 模組中，Applicative 這個 Typeclass 的 <*> 函式型態就是如此定義：

class (Functor f) => Applicative f where   
    pure :: a -> f a   
    (<*>) :: f (a -> b) -> f a -> f b

一個 Applicative 也是一個 Functor，這不難理解，回憶一下 Functor 中 fmap 的型態是 (a -> b) -> f a -> f b，行為上是一樣的，就差在一個是 f (a -> b)，一個是 (a -> b)，而 pure 就是將 (a -> b) 對應至 f (a -> b) 時使用，實際上，Maybe 實現了 Applicative 的行為：

instance Applicative Maybe where   
    pure = Just   
    (Just f) <*> something = fmap f something
    Nothing <*> _ = Nothing

<*> 在實現時，其實以上頭的 op 是一樣的，因此，你可以直接如下操作：

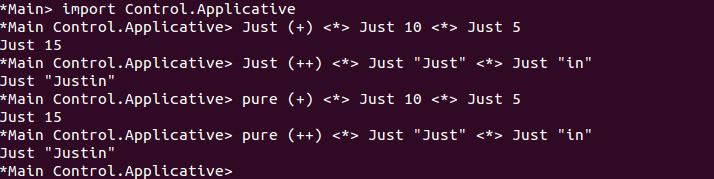
Maybe Applicative

從上頭的實作中，你可以看到，<*> 不過就是使用 fmap，如果你對 fmap 使用 Infix 的方式的話，就會像是：

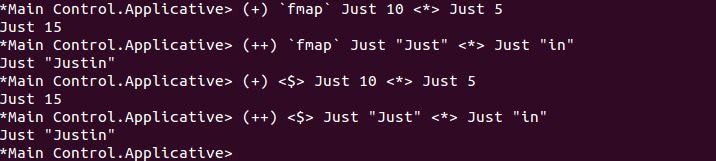
Maybe Applicative

<$> 是 Control.Applicative 模組中定義的函式，它就是 Infix 版本的 fmap：

(<$>) :: (Functor f) => (a -> b) -> f a -> f b   
f <$> x = fmap f x

看來不錯，我們一開始的需求是想要能夠做出像 add (Just 10) (Just 5) 這類的動作，而 (+) <$> Just 10 <*> Just 5 看來就是我們想要的，儘管中間多了 <$>、<*> 這些符號（也就是函式名稱），這說明了 Applicative 的行為，一個 Applicative 實例，要能被函式套用後得到另一個 Applicative。

一個實現了 Applicative 的實例也是個盒子，<*>隱藏了若干運算，兩個參數型態 f (a -> b) 與 f a 表示，函式 a -> b 與值 a，都必須是在 f 這個情境（Context）中，這樣它才能取出 f 中的東西進行運算，pure 的作用，正是將 a -> b 放到 f 中，也就是你在其他文件中常看到的描述「將值放到（運算）情境」。

以 Maybe Applicative 來說，<*> 隱藏了一些有無值處理的運算，兩個參數型態 Maybe (a -> b) 與 Maybe a，這表示函式 a -> b 與值 a，都必須是在 Maybe （這個情境）之中，這樣它才能取出 Maybe 中的東西進行運算，而 pure 的作用，正是將 a -> b 放到 Maybe，其他文件中常見的描述就是「將函式放到（運算）情境」。

更白話來說，因為是處理 Maybe，所以你的函式也要放到 Maybe 中啦！

List Applicative

記得上面說過，我們希望 add ["Justin", "Monica", "Irene"] ["Happy", "Lucky", "Healthy"] 而得到 ["JustinHappy", "JustinLucky", "JustinHealthy", "MonicaHappy", "MonicaLucky", "MonicaHealthy", "IreneHappy", "IreneLucky", "IreneHealthy"] 嗎？你可以這麼做：

List Applicative

也就是說，List 也實現了 Applicative 的行為：

instance Applicative [] where   
    pure x = [x]   
    fs <*> xs = [f x | f <- fs, x <- xs]

因為是處理 List，所以你需要 pure 將指定的函式也放到 List，你也可以這麼使用：

List Applicative

那麼，pure (+) <*> [1, 2, 3] 會是什麼結果呢？

List Applicative

pure (+) <*> [1, 2, 3] 的結果是個 List，型態是 [Integer -> Integer]，也就是一個裝著函式的 List，既然如此，那麼直接給 <*> 一個裝著函式的 List 的函式也可以！別忘了，多參數函式是由單參數函式組成，可以部份套用，因此也可以這麼做：

List Applicative

一個 List Applicative 在被函式套用後而得到另一個 List Applicative 的過程中，隱藏了 List Comprehension 的運算，也就是說，視情況而定（像是可讀性），你可以用它來取代 List Comprehension，例如：

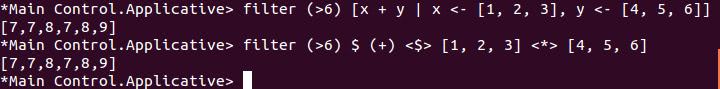
List Applicative

在上面的例子中，Applicative 的風格少了一些變數，不過多了 <$> 與 <*>，可讀性見人見智，如果你（或共事的其他人）不知道 Applicative 隱藏了什麼，或看不懂 <$> 與 <*> 是啥，List Comprehension 的寫法也許會比較好。

IO Applicative

那麼，IO 會是個 Applicative 嗎？想想看，如果你有兩個 IO String，像是從兩個檔案分別讀入了內容，或許你會想將兩個串接在一起，得到一個 IO String，例如：

readFiles :: FilePath -> FilePath -> IO [Char]
readFiles file1 file2 = do
    content1 <- readFile file1
    content2 <- readFile file2
    return (content1 ++ content2)

指定函式，套用至兩個 IO String，得到一個 IO String，看來就是 Applicative 的行為，IO 確實是 Applicative 的實例，因此，readFiles 函式可以更簡潔地實現為：

import Control.Applicative

readFiles :: FilePath -> FilePath -> IO [Char]
readFiles file1 file2 = (++) <$> readFile file1 <*> readFile file2

來看看 IO 如何實現 Applicative：

instance Applicative IO where   
    pure = return   
    a <*> b = do   
        f <- a   
        x <- b   
        return (f x)

pure 的實現就是 return，這會將指定的函式置入 IO 之中，要將 IO 結果使用指定函式處理，就可以使用這種風格。