說明
方陣的維度整體來看是偶數,但是其實是一個奇數乘以一個偶數,例如6X6,其中6=2X3,我們也稱這種方陣與單偶數方陣。解法
如果您會解奇數魔術方陣,要解這種方陣也就不難理解,首先我們令n=2(2m+1),並將整個方陣看作是數個奇數方陣的組合,如下所示: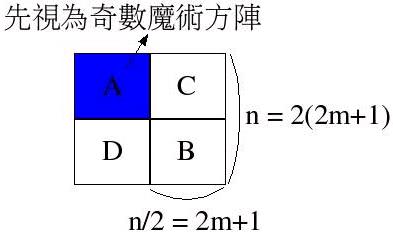
首先依序將A、B、C、D四個位置,依奇數方陣的規則填入數字,填完之後,方陣中各行的和就相同了,但列與對角線則否,此時必須在A-D與C- B之間,作一些對應的調換,規則如下:
- 將A中每一列(中間列除外)的頭m個元素,與D中對應位置的元素調換。
- 將A的中央列、中央那一格向左取m格,並與D中對應位置對調
- 將C中每一列的倒數m-1個元素,與B中對應的元素對調
舉個實例來說,如何填6X6方陣,我們首先將之分解為奇數方陣,並填入數字,如下所示:
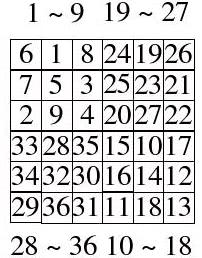
接下來進行互換的動作,互換的元素以不同顏色標示,如下:
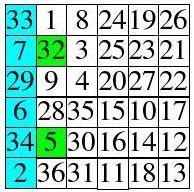
由於m-1的數為0,所以在這個例子中,C-B部份並不用進行對調。
實作:C Java Python Scala Ruby
#include <stdio.h>
#include <stdlib.h>
#define N 6
#define SWAP(x,y) {int t; t = x; x = y; y = t;}
void magic_o(int [][N], int);
void exchange(int [][N], int);
int main(void) {
int square[N][N] = {0};
magic_o(square, N/2);
exchange(square, N);
int i, j;
for(i = 0; i < N; i++) {
for(j = 0; j < N; j++)
printf("%2d ", square[i][j]);
printf("\n");
}
return 0;
}
void magic_o(int square[][N], int n) {
int row = 0;
int column = n / 2;
int count;
for(count = 1; count <= n*n; count++) {
square[row][column] = count; // 填A
square[row+n][column+n] = count + n*n; // 填B
square[row][column+n] = count + 2*n*n; // 填C
square[row+n][column] = count + 3*n*n; // 填D
if(count % n == 0)
row++;
else {
row = (row == 0) ? n - 1 : row - 1 ;
column = (column == n-1) ? 0 : column + 1;
}
}
}
void exchange(int x[][N], int n) {
int m = n / 4;
int m1 = m - 1;
int i, j;
for(i = 0; i < n/2; i++) {
if(i != m) {
for(j = 0; j < m; j++) // 處理規則 1
SWAP(x[i][j], x[n/2+i][j]);
for(j = 0; j < m1; j++) // 處理規則 2
SWAP(x[i][n-1-j], x[n/2+i][n-1-j]);
}
else { // 處理規則 3
for(j = 1; j <= m; j++)
SWAP(x[m][j], x[n/2+m][j]);
for(j = 0; j < m1; j++)
SWAP(x[m][n-1-j], x[n/2+m][n-1-j]);
}
}
}
public class Matrix {
public static int[][] magic(int n) {
int[][] square = new int[n][n];
magic_o(square, n/2);
exchange(square, n);
return square;
}
private static void magic_o(int[][] square, int n) {
int row = 0;
int column = n / 2;
for(int count = 1; count <= n*n; count++) {
square[row][column] = count; // 填A
square[row+n][column+n] = count + n*n; // 填B
square[row][column+n] = count + 2*n*n; // 填C
square[row+n][column] = count + 3*n*n; // 填D
if(count % n == 0)
row++;
else {
row = (row == 0) ? n - 1 : row - 1 ;
column = (column == n-1) ? 0 : column + 1;
}
}
}
private static void exchange(int[][] x, int n) {
int m = n / 4;
int m1 = m - 1;
for(int i = 0; i < n/2; i++) {
if(i != m) {
for(int j = 0; j < m; j++) // 處理規則 1
swap(x, i, j, n/2+i, j);
for(int j = 0; j < m1; j++) // 處理規則 2
swap(x, i, n-1-j, n/2+i, n-1-j);
}
else { // 處理規則 3
for(int j = 1; j <= m; j++)
swap(x, m, j, n/2+m, j);
for(int j = 0; j < m1; j++)
swap(x, m, n-1-j, n/2+m, n-1-j);
}
}
}
private static void swap(int[][] number, int i, int j, int k, int l) {
int t = number[i][j];
number[i][j] = number[k][l];
number[k][l] = t;
}
public static void main(String[] args) {
int[][] magic = Matrix.magic(6);
for(int[] row : magic) {
for(int number: row) {
System.out.printf("%2d ", number);
}
System.out.println();
}
}
}
def magic(n):
square = []
for i in range(n):
square.append([0] * n)
magic_o(square, n // 2)
exchange(square, n)
return square
def magic_o(square, n):
row = 0
column = n // 2
for count in range(1, n ** 2 + 1):
square[row][column] = count; # 填A
square[row + n][column + n] = count + n * n; # 填B
square[row][column + n] = count + 2 * n * n; # 填C
square[row + n][column] = count + 3 * n * n; # 填D
if count % n == 0:
row += 1
else:
row = n - 1 if row == 0 else row - 1
column = 0 if column == n - 1 else column + 1
def exchange(x, n):
m = n // 4
m1 = m - 1
for i in range(n // 2):
if i != m:
for j in range(m):
x[i][j], x[n // 2 + i][j] = \
x[n // 2 + i][j], x[i][j]
for j in range(m1):
x[i][n - 1 - j], x[n // 2 + i][n - 1 -j] = \
x[n // 2 + i][n - 1 - j], x[i][n - 1 - j]
else:
for j in range(1, m + 1):
x[m][j], x[n // 2 + m][j] = \
x[n // 2 + m][j], x[m][j]
for j in range(m1):
x[m][n - 1 - j], x[n // 2 + m][n - 1 -j] = \
x[n // 2 + m][n - 1 -j], x[m][n - 1 - j]
matrix = magic(6)
print(matrix)
object Matrix {
def magic(n: Int) = {
val square = new Array[Array[Int]](n, n)
magic_o(square, n / 2)
exchange(square, n)
square
}
private def magic_o(square: Array[Array[Int]], n: Int) {
var row = 0
var column = n / 2
for(count <- 1 to n * n ) {
square(row)(column) = count
square(row+n)(column+n) = count + n*n;
square(row)(column+n) = count + 2*n*n;
square(row+n)(column) = count + 3*n*n;
if(count % n == 0) row += 1
else {
row = if(row == 0) n - 1 else row - 1
column = if(column == n-1) 0 else column + 1
}
}
}
private def exchange(x: Array[Array[Int]], n: Int) {
val m = n / 4
val m1 = m - 1
for(i <- 0 until n / 2) {
if(i != m) {
for(j <- 0 until m) swap(x, i, j, n/2+i, j)
for(j <- 0 until m1) swap(x, i, n-1-j, n/2+i, n-1-j)
}
else {
for(j <- 1 to m) swap(x, m, j, n/2+m, j)
for(j <- 0 until m1) swap(x, m, n-1-j, n/2+m, n-1-j)
}
}
}
private def swap(number: Array[Array[Int]],
i: Int, j: Int, k: Int, l: Int) {
val t = number(i)(j)
number(i)(j) = number(k)(l)
number(k)(l) = t
}
}
Matrix.magic(6).foreach(row => {
row.foreach(number => printf("%2d ", number))
println()
})
def magic(n)
square = Array.new(n) {
Array.new(n, 0)
}
magic_o(square, n / 2)
exchange(square, n)
square
end
def magic_o(square, n)
row = 0
column = n / 2
1.upto(n ** 2) { |count|
square[row][column] = count; # 填A
square[row + n][column + n] = count + n * n; # 填B
square[row][column + n] = count + 2 * n * n; # 填C
square[row + n][column] = count + 3 * n * n; # 填D
if count % n == 0
row += 1
else
row = (row == 0) ? n - 1 : row - 1
column = (column == n - 1) ? 0 : column + 1
end
}
end
def exchange(x, n)
m = n / 4
m1 = m - 1
(n / 2).times { |i|
if i != m
m.times { |j|
x[i][j], x[n / 2 + i][j] =
x[n / 2 + i][j], x[i][j]
}
m1.times { |j|
x[i][n - 1 - j], x[n / 2 + i][n - 1 -j] =
x[n / 2 + i][n - 1 - j], x[i][n - 1 - j]
}
else
1.upto(m) { |j|
x[m][j], x[n / 2 + m][j] =
x[n / 2 + m][j], x[m][j]
}
m1.times { |j|
x[m][n - 1 - j], x[n / 2 + m][n - 1 -j] =
x[n / 2 + m][n - 1 -j], x[m][n - 1 - j]
}
end
}
end
matrix = magic(6)
p matrix

