快速排序法（三）

說明

之前說過軸的選擇是快速排序法的效率關鍵之一，在這邊的快速排序法的軸選擇方式更加快了快速排序法的效率，它是來自演算法名書 Introduction to Algorithms 之中。

解法

先說明這個快速排序法的概念，它以最右邊（或最左邊）的值s作比較的標準，將整個數列分為三個部份，一個是小於s的部份，一個是大於s的部份，一個是未處理的部份，如下所示：

在排序的過程中，i 與 j 都會不斷的往右進行比較與交換，最後數列會變為以下的狀態：

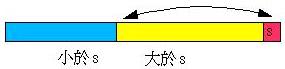
然後將s的值置於中間，接下來就以相同的步驟會左右兩邊的數列進行排序的動作，如下所示：

整個演算的過程，直接摘錄書中的虛擬碼來作說明：

QUICKSORT(A, p, r) 
    if p < r 
        then q <- PARTITION(A, p, r) 
                 QUICKSORT(A, p, q-1) 
                 QUICKSORT(A, q+1, r) 
end QUICKSORT 

PARTITION(A, p, r) 
    x <- A[r] 
    i <- p-1 
    for j <- p to r-1 
        do if A[j] <= x 
                 then  i <- i+1 
                         exchange A[i]<->A[j] 
    exchange A[i+1]<->A[r] 
    return i+1 
end PARTITION

一個實際例子的演算如下所示：

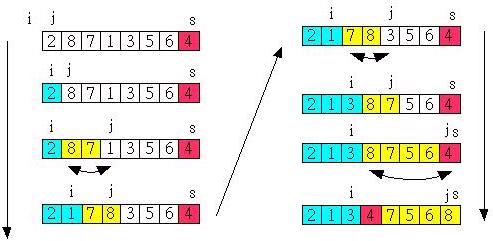
實作：C Java Python Scala Ruby

#include <stdio.h> 
#include <stdlib.h> 
#include <time.h> 
#define MAX 10 
#define SWAP(x,y) {int t; t = x; x = y; y = t;} 

int partition(int[], int, int); 
void quickSort(int[], int, int); 

int main(void) { 
    srand(time(NULL)); 
    
    int number[MAX] = {0}; 

    printf("排序前："); 
    int i;
    for(i = 0; i < MAX; i++) { 
        number[i] = rand() % 100; 
        printf("%d ", number[i]); 
    } 

    quickSort(number, 0, MAX-1); 

    printf("\n排序後："); 
    for(i = 0; i < MAX; i++) 
        printf("%d ", number[i]); 
    
    printf("\n"); 

    return 0; 
} 

int partition(int number[], int left, int right) { 
    int i = left - 1; 
    int j;
    for(j = left; j < right; j++) { 
        if(number[j] <= number[right]) { 
            i++; 
            SWAP(number[i], number[j]); 
        } 
    } 

    SWAP(number[i+1], number[right]); 
    return i+1; 
} 

void quickSort(int number[], int left, int right) { 
    if(left < right) { 
        int q = partition(number, left, right); 
        quickSort(number, left, q-1); 
        quickSort(number, q+1, right); 
    } 
}

Java

public class Sort {
    public static void quick(int[] number) {
        sort(number, 0, number.length-1);
    }
    
    private static void sort(int[] number, int left, int right) {
        if(left < right) { 
            int q = partition(number, left, right); 
            sort(number, left, q-1); 
            sort(number, q+1, right); 
        } 

    }

    private static int partition(int number[], int left, int right) {  
        int i = left - 1; 
        for(int j = left; j < right; j++) { 
            if(number[j] <= number[right]) { 
                i++; 
                swap(number, i, j); 
            } 
        } 
        swap(number, i+1, right); 
        return i+1; 
    } 

    private static void swap(int[] number, int i, int j) {
        int t = number[i]; 
        number[i] = number[j]; 
        number[j] = t;
    }
}

Python

def sort(lst):
    if len(lst) <= 1:
        return lst
    pivot = lst.pop(0)
    before = [i for i in lst if i < pivot]
    after = [i for i in lst if i >= pivot]
    return sort(before) + [pivot] + sort(after)

Scala

object Sort {
    def quick(list: List[Int]): List[Int] = {
       list match {
           case Nil => Nil     
           case x::xs =>        
           val (before,after) = xs partition (_ < x)
           quick(before) ++ (x :: quick(after))
       }
    }
}

Ruby

class Array
    def comprehend(&block)
        return self if block.nil?
        self.collect(&block).compact
    end
end

def quick(lst)
    case
    when lst.length <= 1
        lst
    when pivot = lst.shift
        before = lst.comprehend { |i| i if i < pivot}
        after = lst.comprehend { |i| i if i >= pivot}
        quick(before) + [pivot] + quick(after)
    end
end