快速排序法（一）

說明

快速排序法（Quick sort）是目前常用的排序方法之一，雖然快速排序法在最差狀況下會達O(n²)，但在多數情況下，快速排序法具有相當不錯的效率表現。

快速排序法精神是分而治之，以昇冪為例，基本上就將數列分為小於S的子數列、S與大於S的子數列，接著對兩個子數列作相同處理，S稱為軸心，不同的快速排序法實作，差別在於S的選擇與分出子數列的方式。

解法

這邊介紹的第一個快速排序法版本，其S的選擇是數列開頭，並同時由左而右及由右至左分出子數列：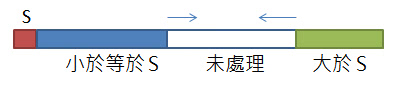

尚未處理的數列會是在中間被逐步消化完畢：

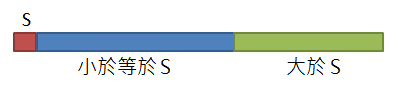
接著將S置於兩個子數列之間。

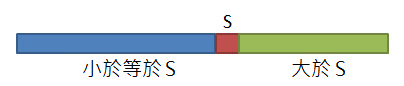
此時S左邊都是小於等於S，右邊都是大於S，再分別對這兩個子數列做遞迴處理。

實作：C Java Python Scala Ruby JavaScript Haskell

#include <stdio.h> 
#include <stdlib.h> 
#define LEN 10 
#define SWAP(x,y) {int t; t = x; x = y; y = t;} 

void sort(int*, int, int(*)(int, int)); 
void quickSort(int*, int, int, int(*)(int, int)); 
void print(int*, int len);
int ascending(int, int);
int descending(int, int);

int main(void) { 
    int number[LEN] = {10, 9, 1, 2, 5, 3, 8, 7, 12, 11};
    
    sort(number, LEN, ascending); 
    print(number, LEN);
    
    sort(number, LEN, descending); 
    print(number, LEN);

    return 0; 
} 

void sort(int* number, int len, int(*comp)(int, int)) {
    quickSort(number, 0, len - 1, comp); 
}

void quickSort(int* number, int left, int right, int(*comp)(int, int)) {
    if(left < right) {
        int axis = partition(number, left, right, comp); 
        quickSort(number, left, axis - 1, comp);  
        quickSort(number, axis + 1, right, comp); 
    } 
}

int partition(int* number, int left, int right, int(*comp)(int, int)) {
    int s = number[left];
    int axis = partitionUnprocessed(number, left + 1, right, s, comp);
    SWAP(number[left], number[axis]); 
    return axis;
}

int partitionUnprocessed(int* number, int left, int right, 
                         int s, int(*comp)(int, int)) {
    int i = lookRight(number, left, right, s, comp);
    int j = lookLeft(number, right, i, s, comp);
    if(i < j) {
        SWAP(number[i], number[j]); 
        return partitionUnprocessed(number, i + 1, j - 1, s, comp);
    }
    return j;
}

int lookRight(int* number, int from, int to, int s, int(*comp)(int, int)) {
    int i = from;
    while(i < to + 1 && comp(number[i], s) <= 0) { i++; }
    return i;
}

int lookLeft(int* number, int from, int to, int s, int(*comp)(int, int)) {
    int j = from;
    while(j > to - 1 && comp(number[j], s) > 0) { j--; }
    return j;
}

void print(int* arr, int len) {
    int i;
    for(i = 0; i < len; i++) { printf("%d ", arr[i]); } 
    printf("\n");
}

int ascending(int a, int b) { return a - b; }
int descending(int a, int b) { return -ascending(a, b); }

Java

import java.util.*;
import static java.lang.System.out;
import static java.util.Collections.swap;

public class Sort {
    public static <T extends Comparable<? super T>> 
        int ascending(T t1, T t2) {  return t1.compareTo(t2); }

    public static <T extends Comparable<? super T>> 
        int descending(T t1, T t2) { return -ascending(t1, t2); }
    
    public static <T extends Comparable<? super T>> 
        void sort(List<T> list) { sort(list, Sort::ascending); }

    public static <T> void sort(
        List<T> list, Comparator<? super T> c) {
         quickSort(list, 0, list.size() - 1, c);
    }

    private static <T> void quickSort(
        List<T> list, int left, int right, Comparator<? super T> c) {
        if(left < right) {
            int axis = partition(list, left, right, c); 
            quickSort(list, left, axis - 1, c);  
            quickSort(list, axis + 1, right, c); 
        }
    }

    private static <T> int partition(List<T> list, 
                      int left, int right, Comparator<? super T> c) {
        T s = list.get(left);
        int axis = partitionUnprocessed(list, left + 1, right, s, c);
        swap(list, left, axis);
        return axis;
    }

    private static <T> int partitionUnprocessed(List<T> list, 
                      int left, int right, T s, Comparator<? super T> c) {
        int i = lookRight(list, left, right, s, c);
        int j = lookLeft(list, right, i, s, c);
        if(i < j) {
            swap(list, i, j);
            return partitionUnprocessed(list, i + 1, j - 1, s, c);
        }
        return j;
    }

    private static <T> int lookRight(List<T> list, 
                        int from, int to, T s, Comparator<? super T> c) {
        int i = from;
        while(i < to + 1 && c.compare(list.get(i), s) <= 0) { i++; }
        return i;
    }

    private static <T> int lookLeft(List<T> list, 
                        int from, int to, T s, Comparator<? super T> c) {
        int j = from;
        while(j > to - 1 && c.compare(list.get(j), s) > 0) { j--; }
        return j;
    }
        
    public static void main(String[] args) {
        List<Integer> list = 
            new ArrayList<>(Arrays.asList(10, 9, 1, 2, 5, 3, 8, 7, 12, 11));
        
        sort(list);
        out.println(list);
        
        sort(list, Sort::descending);
        out.println(list);
    }
}

Python

def ascending(a, b): return a - b
def descending(a, b): return -ascending(a, b)

def quickSort(xs, comp = ascending):
    if not xs:
        return []
    else:
        lefter, axis, righter = partition(xs, comp)
        return quickSort(lefter, comp) + axis + quickSort(righter, comp)

def partition(xs, comp):
    lefter, righter = partitionUnpressed(
        xs[1:], 0, len(xs[1:]) - 1, xs[0], comp)
    return (lefter, [xs[0]], righter)

def partitionUnpressed(xs, left, right, s, comp):
    i = lookRight(xs, left, right, s, comp)
    j = lookLeft(xs, right, i, s, comp)
    if i < j:
        outerLefter = xs[left:i] + [xs[j]]
        outerRightr = [xs[i]] + xs[j + 1 : right + 1]
        innerLefter, innerRighter = partitionUnpressed(
            xs, i + 1, j - 1, s, comp)
        return (outerLefter + innerLefter, innerRighter + outerRightr)
    return (xs[left : i], xs[j + 1 : right + 1])

def lookRight(xs, i, to, s, comp):
    return (lookRight(xs, i + 1, to, s, comp) 
               if i < to + 1 and comp(xs[i], s) <= 0 else i)

def lookLeft(xs, j, to, s, comp):
    return (lookLeft(xs, j - 1, to, s, comp) 
               if j > to - 1 and comp(xs[j], s) > 0 else j)

list = [10, 9, 1, 2, 5, 3, 8, 7, 12, 11]

print(quickSort(list))
print(quickSort(list, descending))

Scala

object Sort {
    def quick[T](xs: List[T], compare: (T, T) => Boolean): List[T] = {
        if(xs.isEmpty) Nil
        else {
            val (lefter, axis, righter) = partition(xs, compare)
            quick(lefter, compare) ++ axis ++ quick(righter, compare)
        }
    }

    def partition[T](xs: List[T], compare: (T, T) => Boolean) = {
        val (lefter, righter) = partitionUnpressed(
            xs.tail, 0, xs.size - 2, xs.head, compare)
        (lefter, List(xs.head), righter)
    }

    def partitionUnpressed[T](xs: List[T], left: Int, right: Int, 
                s: T, compare: (T, T) => Boolean): (List[T], List[T])= {
        val i = lookRight(xs, left, right, s, compare)
        val j = lookLeft(xs, right, i, s, compare)
        if(i < j) {
            val outerLefter = xs.slice(left, i) ++ List(xs(j))
            val outerRighter = xs(i) :: xs.slice(j + 1, right + 1)
            val (innerLefter, innerRighter) = 
                partitionUnpressed(xs, i + 1, j - 1, s, compare)
            (outerLefter ++ innerLefter, innerRighter ++ outerRighter)
        } else {
            (xs.slice(left, i), xs.slice(j + 1, right + 1))
        }
    }

    def lookRight[T](xs: List[T], i: Int, to: Int, 
                s: T, compare: (T, T) => Boolean): Int = {
        if(i < to + 1 && compare(xs(i), s)) 
            lookRight(xs, i + 1, to, s, compare) 
        else i
    }

    def lookLeft[T](xs: List[T], j: Int, to: Int, 
                s: T, compare: (T, T) => Boolean): Int = {
        if(j > to - 1 && !compare(xs(j), s)) 
            lookLeft(xs, j - 1, to ,s, compare) 
        else j
    }
}

val list = List(10, 9, 1, 2, 5, 3, 8, 7, 12, 11)

println(Sort.quick[Int](list, _ > _))
println(Sort.quick[Int](list, _ < _))

Ruby

class Sort
    @@ascending = ->(a, b) { a - b }
    @@descending = ->(a, b) { -@@ascending.call(a, b) }
    
    def self.ascending; @@ascending end
    def self.descending; @@descending end
    
    def self.quick(xs, comp)
        if xs.empty?
            []
        else
            lefter, axis, righter = *partition(xs, comp)
            quick(lefter, comp) + axis + quick(righter, comp)
        end
    end

    def self.partition(xs, comp)
        (head, *tail) = xs
        lefter, righter = *partitionUnpressed(
            tail, 0, xs.size - 2, head, comp)
        [lefter, [head], righter]
    end
    private_class_method :partition

    def self.partitionUnpressed(xs, left, right, s, comp)
        i = lookRight(xs, left, right, s, comp)
        j = lookLeft(xs, right, i, s, comp)
        if i < j
            outerLefter = xs[left...i] + [xs[j]]
            outerRightr = [xs[i]] + xs[j + 1...right + 1]
            innerLefter, innerRighter = *partitionUnpressed(
                xs, i + 1, j - 1, s, comp)
            [outerLefter + innerLefter, innerRighter + outerRightr]
        else
            [xs[left...i], xs[j + 1...right + 1]]
        end
    end
    private_class_method :partitionUnpressed

    def self.lookRight(xs, i, to, s, comp)
        (i < to + 1 and comp.call(xs[i], s) <= 0) ? 
            lookRight(xs, i + 1, to, s, comp) : i
    end
    private_class_method :lookRight

    def self.lookLeft(xs, j, to, s, comp)
        (j > to - 1 and comp.call(xs[j], s) > 0) ? 
            lookLeft(xs, j - 1, to, s, comp) : j
    end
    private_class_method :lookLeft
end

list = [10, 9, 1, 2, 5, 3, 8, 7, 12, 11]

print(Sort.quick(list, Sort.ascending).to_s + "\n")
print(Sort.quick(list, Sort.descending).to_s + "\n")

JavaScript

function ascending(a, b) {return a - b;}
function descending(a, b) {return -ascending(a, b);}

var quickSort = function() {
    function swap(list, i, j) {
        var ele = list[i];
        list[i] = list[j];
        list[j] = ele;
    }

    function quick(list, left, right, c) {
        if(left < right) {
            var axis = partition(list, left, right, c); 
            quick(list, left, axis - 1, c);  
            quick(list, axis + 1, right, c); 
        }
    }
    
    function partition(list, left, right, c) {
        var s = list[left];
        var axis = partitionUnprocessed(list, left + 1, right, s, c);
        swap(list, left, axis);
        return axis;
    }

    function partitionUnprocessed(list, left, right, s, c) {
        var i = lookRight(list, left, right, s, c);
        var j = lookLeft(list, right, i, s, c);
        if(i < j) {
            swap(list, i, j);
            return partitionUnprocessed(list, i + 1, j - 1, s, c);
        }
        return j;
    }

    function lookRight(list, from, to, s, c) {
        var i = from;
        while(i < to + 1 && c(list[i], s) <= 0) { i++; }
        return i;
    }

    function lookLeft(list, from, to, s, c) {
        var j = from;
        while(j > to - 1 && c(list[j], s) > 0) { j--; }
        return j;
    }

    return function(list, c) {
        return quick(list, 0, list.length - 1, c);
    };
}();

var list = [10, 9, 1, 2, 5, 3, 8, 7, 12, 11];

quickSort(list, ascending);
print(list);

quickSort(list, descending);
print(list);

Haskell

ascending a b = a - b
descending a b = -ascending a b

slice from to xs = take (to - from) (drop from xs)

quickSort xs comp =
    if xs == [] then []
    else
        let (lefter, axis, righter) = partition xs comp
        in (quickSort lefter comp) ++ axis ++ (quickSort righter comp)

partition xs comp =
    let (lefter, righter) = 
            partitionUnpressed (tail xs) 0 (length xs - 2) (head xs) comp
    in (lefter, [head xs], righter)

partitionUnpressed xs left right s comp =
    let i = lookRight xs left right s comp
        j = lookLeft xs right i s comp
    in
        if i < j then
            let outerLefter = (slice left i xs) ++  [xs !! j]
                outerRighter = (xs !! i) : slice (j + 1) (right + 1) xs
                (innerLefter, innerRighter) = 
                    partitionUnpressed xs (i + 1) (j - 1) s comp
            in (outerLefter ++ innerLefter, innerRighter ++ outerRighter)
        else (slice left i xs, slice (j + 1) (right + 1) xs)


lookRight xs i to s comp =
    if i < to + 1 && (comp (xs !! i) s) <= 0
        then lookRight xs (i + 1) to s comp
        else i

lookLeft xs j to s comp = 
    if j > to - 1 && (comp (xs !! j) s) > 0
        then lookLeft xs (j - 1) to s comp
        else j

main = sequence [print \$ quickSort xs ascending, 
                 print \$ quickSort xs descending]
    where xs = [10, 9, 1, 2, 5, 3, 8, 7, 12, 11]