奇數魔方陣

說明

將1到n(為奇數)的數字排列在nxn的方陣上，且各行、各列與各對角線的和必須相同，如下所示：

解法

填魔術方陣的方法以奇數最為簡單，第一個數字放在第一行第一列的正中央，然後向右(左)上填，如果右(左)上已有數字，則向下填，如下圖所示：

一般程式語言的陣列索引多由0開始，為了計算方便，我們利用索引1到n的部份，而在計算是向右(左)上或向下時，我們可以將索引值除以n值，如果得到餘數為1就向下，否則就往右(左)上，原理很簡單，看看是不是已經在同一列上繞一圈就對了。

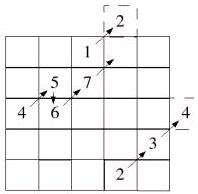
實作：C Java Python Scala Ruby

#include <stdio.h> 
#include <stdlib.h> 

#define N 5 

int main(void) { 
    int square[N+1][N+1] = {0}; 

    int i = 0; 
    int j = (N+1) / 2; 
    int key;
    for(key = 1; key <= N*N; key++) { 
        if((key % N) == 1) 
            i++; 
        else { 
            i--; 
            j++; 
        } 

        if(i == 0) 
            i = N; 
        if(j > N) 
            j = 1; 

        square[i][j] = key; 
    } 

    int m, n;
    for(m = 1; m <= N; m++) { 
        for(n = 1; n <= N; n++) 
            printf("%2d ", square[m][n]); 
    } 

    return 0; 
}

Java

public class Matrix {
    public static int[][] magic(int n) {
        int[][] square = new int[n+1][n+1]; 

        for(int i = 0, j = (n + 1) / 2, key = 1; key <= n*n; key++) { 
            if((key % n) == 1) i++; 
            else { i--; j++; } 

            if(i == 0) i = n; 
            if(j > n) j = 1; 

            square[i][j] = key; 
        }
        
        int[][] matrix = new int[n][n];
        
        for(int k = 0; k < matrix.length; k++) {
           for(int l = 0; l < matrix[0].length; l++) {
               matrix[k][l] = square[k+1][l+1];
           }
        }
        
        return matrix;
    }
    
    public static void main(String[] args) {
        for(int[] row : Matrix.magic(5)) {
            for(int number: row) {
                System.out.printf("%2d ", number);
            }
            System.out.println();
         }
    }
}

Python

def magic(n):
    square = []
    for i in range(n + 1):
        square.append([0] * (n + 1))
    i = 0
    j = (n + 1) // 2
    for key in range(1, n ** 2 + 1):
        if key % n == 1:
            i += 1
        else:
            i -= 1
            j += 1
        if i == 0:
            i = n
        if j > n:
            j = 1
        square[i][j] = key
    matrix = []
    for i in range(n):
        matrix.append([0] * n)
    for k in range(len(matrix)):
        for l in range(len(matrix[0])):
            matrix[k][l] = square[k + 1][l + 1]
    return matrix

matrix = magic(5)
print(matrix)

Scala

object Matrix {
    def magic(n: Int) = {
        val square = new Array[Array[Int]](n + 1, n + 1)
        var i = 0
        var j = (n + 1) / 2
        for(key <- 1 to n * n) {
            if((key % n) == 1) i += 1
            else { i -= 1; j += 1}

            if(i == 0) i = n
            if(j > n) j = 1
            
            square(i)(j) = key
        }
        
        val matrix = new Array[Array[Int]](n, n)
        for(k <- 0 until matrix.length; l <- 0 until matrix(0).length) {
            matrix(k)(l) = square(k + 1)(l + 1)
        }
        matrix
    }
}

Matrix.magic(5).foreach(row => {
    row.foreach(number => printf("%2d ", number))
    println()
})

Ruby

def magic(n)
    square = Array.new(n + 1) {
        Array.new(n + 1, 0)
    }
    i = 0
    j = (n + 1) / 2
    1.upto(n ** 2) { |key|
        if key % n == 1
            i += 1
        else
            i -= 1
            j += 1
        end
        if i == 0
            i = n
        end
        if j > n
            j = 1
        end
        square[i][j] = key
    }
    matrix = Array.new(n) {
        Array.new(n, 0)
    }
    matrix.length.times { |k|
        matrix[0].length.times { |l|
            matrix[k][l] = square[k + 1][l + 1]            
        }
    }
    matrix
end

matrix = magic(5)
p matrix