插補搜尋法

說明

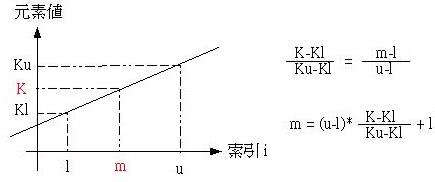
如果卻搜尋的資料分佈平均的話，可以使用插補（Interpolation）搜尋法來進行搜尋，在搜尋的對象大於500時，插補搜尋法會比二分搜尋法來的快速。

解法

插補搜尋法是以資料分佈的近似直線來作比例運算，以求出中間的索引並進行資料比對，如果取出的值小於要尋找的值，則提高下界，如果取出的值大於要尋找的值，則降低下界，如此不斷的減少搜尋的範圍，所以其本原則與二分搜尋法是相同的，至於中間值的尋找是透過比例運算，如下所示，其中K是指定要尋找的對象，而m則是可能的索引值：

實作：C Java Python Scala Ruby

#include <stdio.h> 
#include <stdlib.h> 
#include <time.h> 
#define MAX 10 
#define SWAP(x,y) {int t; t = x; x = y; y = t;} 

void quickSort(int[], int, int); 
int interpolationSearch(int[], int); 

int main(void) { 
    srand(time(NULL)); 
    
    int number[MAX] = {0}; 
    
    int i;
    for(i = 0; i < MAX; i++) { 
        number[i] = rand() % 100; 
    } 

    quickSort(number, 0, MAX-1); 

    printf("數列："); 
    for(i = 0; i < MAX; i++) 
        printf("%d ", number[i]); 

    int find;
    printf("\n輸入尋找對象："); 
    scanf("%d", &find); 

    if((i = interpolationSearch(number, find)) >= 0) 
        printf("找到數字於索引 %d ", i); 
    else 
        printf("\n找不到指定數"); 
        
    printf("\n"); 

    return 0; 
} 

int interpolationSearch(int number[], int find) { 
    int low = 0; 
    int upper = MAX - 1; 
    while(low <= upper) { 
        int mid = (upper-low)* 
            (find-number[low])/(number[upper]-number[low]) 
            + low; 
        if(mid < low || mid > upper) 
            break; 
        if(find < number[mid]) 
            upper = mid - 1; 
        else if(find > number[mid]) 
            low = mid + 1; 
        else 
            return mid; 
     } 
     return -1;
} 

void quickSort(int number[], int left, int right) { 
    if(left < right) { 
        int s = number[(left+right)/2]; 
        int i = left - 1; 
        int j = right + 1; 

        while(1) { 
            while(number[++i] < s) ;  // 向右找 
            while(number[--j] > s) ;  // 向左找 
            if(i >= j) 
                break; 
            SWAP(number[i], number[j]); 
        } 

        quickSort(number, left, i-1);   // 對左邊進行遞迴 
        quickSort(number, j+1, right);  // 對右邊進行遞迴 
    } 
}

Java

public class Search {    
    public static int interpolation(int[] number, int des) { 
        int low = 0; 
        int upper = number.length - 1; 

        while(low <= upper) { 
            int mid = (upper-low)*(des-number[low])
                      /(number[upper]-number[low]) + low; 
            if(mid < low || mid > upper) 
                break; 
            if(des < number[mid]) 
                upper = mid - 1; 
            else if(des > number[mid]) 
                low = mid + 1; 
            else 
                return mid; 
        }
        return -1;
    }
    
    public static void main(String[] args) {
        int[] number = {1, 2, 3, 4, 6, 7, 8};
        int find = Search.interpolation(number, 2);
        System.out.println(find >= 0 ? "找到數值於索引" + find : "找不到數值"); 
    }
}

Python

def search(number, des):
    low = 0
    upper = len(number) - 1
    while low <= upper:
        mid = (upper - low) * (des - number[low]) \
               // (number[upper] - number[low]) \
               + low;
        if mid < low or mid > upper:
            break
        if des < number[mid]:
            upper = mid - 1
        elif des > number[mid]:
            low = mid + 1
        else:
            return mid
        
    return -1

number = [1, 4, 2, 6, 7, 3, 9, 8]
number.sort()
find = search(number, 2)
print("找到數值於索引 " + str(find) if find >= 0 else "找不到數值")

Scala

object Search {
    def interpolation(number: Array[Int], des: Int) = {
        var low = 0
        var upper = number.length - 1
        var result = -1
        var isContinue = true
        while(isContinue && low <= upper) {
            val mid = (upper-low)* (des-number(low)) / 
                      (number(upper)-number(low)) + low
            if(mid < low || mid > upper) isContinue = false
            if(des < number(mid))
                upper = mid - 1
            else if(des > number(mid))
                low = mid + 1
            else {
                result = mid
                isContinue = false
            }
        }
        result
    }
}

val number = Array(1, 2, 3, 4, 6, 7, 8)
val find = Search.interpolation(number, 3)
println(if(find >= 0) "找到數值於索引 " + find else "找不到數值")

Ruby

# encoding: Big5
def search(number, des)
    low = 0
    upper = number.length - 1
    while low <= upper
        mid = (upper - low) * (des - number[low]) / 
              (number[upper] - number[low]) + low
        if mid < low || mid > upper
            break
        end
            
        if des < number[mid]
            upper = mid - 1
        elsif des > number[mid]
            low = mid + 1
        else
            return mid
        end
    end
    -1
end

number = [1, 4, 2, 6, 7, 3, 9, 8]
number.sort!
find = search(number, 2)
print find >= 0 ? "找到數值於索引 " + find.to_s : "找不到數值", "\n"