說明
選擇排序法的概念簡單,以降冪為例,每次從未排序部份選一最小值,插入已排序部份的後端,其時間主要花費於在整個未排序部份尋找最小值,如果能讓搜尋最小值的方式加 快,選擇排序法的速率也就可以加快,Heap排序法讓搜尋的路徑由樹根至最後一個樹葉,而不是整個未排序部份,因而稱之為改良的選擇排序法。解法
Heap排序法使用堆積樹(Heap tree),樹是一種資料結構,而堆積樹是一個二元樹,每個父節點最多只有兩個子節點,堆積樹的 父節點若小於子節點,則稱之為最小堆積(Min heap),父節點若大於子節點,則稱之為最大堆積(Max heap),而同一層的子節點則無需理會其大小關係,例如下面就是一個堆積樹: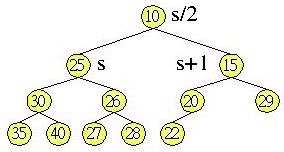
可以使用一維陣列來儲存堆積樹的所有元素與其順序,為了計算方便,使用的起始索引是1而不是0,索引1是樹根位置,如果左子節點儲存在陣列中的索引為s,則其父節點的索引為s/2,而右子節點為s+1,就如上圖所示,將上圖的堆積樹轉換為一維陣列之後如下所示:

首先必須知道如何建立堆積樹,以最小堆積為例,加至堆積樹的元素會先放置在最後一個樹葉節點位置,然後檢查父節點是否小於子節點,將小的元素不斷與父節點交換,直到滿足堆積樹的條件為止,例如在上圖的堆積加入一個元素12,則堆積樹的調整方式如下所示:
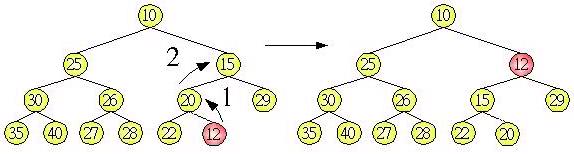
建立好堆積樹之後,樹根一定是所有元素的最小值,排序應用時:
- 將最小值取出
- 調整樹為最小堆積樹
不斷重複以上的步驟,就可以達到排序的效果,最小值取出方式是將樹根與最後一個樹葉節點交換,然後切下樹葉節點,重新調整樹為堆積樹,調整過程中,找出父節點兩子節點中較小的一個進行交換,如下所示:
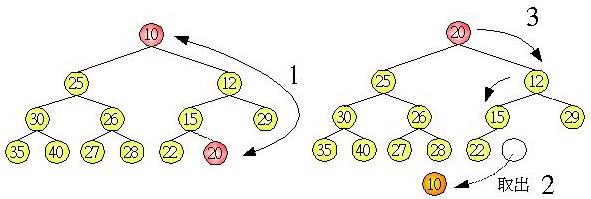
調整完畢後,樹根節點又是最小值了,於是可以重覆這個步驟,再取出最小值,並調整樹為堆積樹,如下所示:
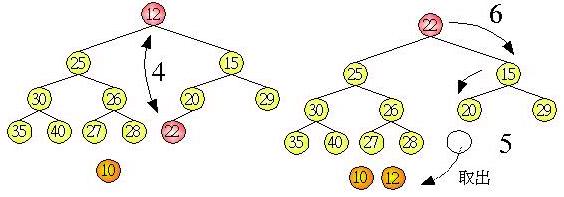
如此重覆步驟之後,由於使用一維陣列來儲存堆積樹,每次將樹葉與樹根交換的動作就是將最小值放至後端的陣列,所以最後陣列就是變為已排序的狀態。
堆積樹在建立時,就樹葉到樹根的路徑來看,是氣泡排序。堆積排序若看每次選出最小值樹根與最後一個樹葉交換,是選擇排序,後續進行調整的過程中,就樹根到樹葉的路徑來看,實際上也在進行氣泡排序。如果以視覺化來看排序過程,已排序部份的出現可很明顯地看出像是選擇排序(參考維基百科上的 動畫圖片),調整過程則沒那麼明顯的視覺效果,因此Heap排序法被稱為改良的選擇排序法。
實作:C Java Python Scala Ruby JavaScript Haskell
#include <stdio.h>
#include <stdlib.h>
#define LEN 10
#define OFFSET 1
#define SWAP(x,y) {int t; t = x; x = y; y = t;}
void heapSort(int*, int len, int(*)(int, int));
void heapTree(int*, int, int(*)(int, int));
void selectFromHeap(int*, int, int(*)(int, int));
void bubbleLeaf(int*, int, int(*)(int, int));
int isBubbleable(int*, int, int, int(*)(int, int));
void bubbleRoot(int*, int, int(*)(int, int));
int idxFromChilds(int*, int, int, int(*)(int, int));
int isRightLeafSuitable(int*, int, int, int(*)(int, int));
void print(int*, int len);
int ascending(int, int);
int descending(int, int);
int main(void) {
int num[LEN] = {10, 9, 1, 2, 5, 3, 8, 7, 12, 11};
heapSort(num, LEN, descending);
print(num, LEN);
heapSort(num, LEN, ascending);
print(num, LEN);
system("PAUSE");
return 0;
}
void heapSort(int* num, int len, int(*compar)(int, int)) {
heapTree(num, len, compar);
selectFromHeap(num, len, compar);
}
void heapTree(int* num, int len, int(*compar)(int, int)) {
int i, end;
for(i = 1, end = len + 1; i < end; i++) { bubbleLeaf(num, i, compar); }
}
void selectFromHeap(int* num, int len, int(*comp)(int, int)) {
int end;
for(end = len; end > OFFSET; end--) {
SWAP(num[1 - OFFSET], num[end - OFFSET]);
bubbleRoot(num, end, comp);
}
}
void bubbleLeaf(int* num, int eleIdx, int(*compar)(int, int)) {
int childIdx, parentIdx;
for(childIdx = eleIdx, parentIdx = eleIdx / 2;
isBubbleable(num, childIdx, parentIdx, compar);
childIdx = parentIdx, parentIdx = childIdx / 2) {
SWAP(num[parentIdx - OFFSET], num[childIdx - OFFSET]);
}
}
int isBubbleable(int* num, int childIdx,
int parentIdx, int(*compar)(int, int)) {
return childIdx > OFFSET &&
compar(num[parentIdx - OFFSET], num[childIdx - OFFSET]) < 0;
}
void bubbleRoot(int* num, int end, int(*comp)(int, int)) {
int parentIdx, childIdx;
for(parentIdx = 0 + OFFSET,
childIdx = idxFromChilds(num, parentIdx, end, comp);
childIdx < end &&
comp(num[childIdx - OFFSET], num[parentIdx - OFFSET]) > 0;
parentIdx = childIdx,
childIdx = idxFromChilds(num, parentIdx, end, comp)) {
SWAP(num[parentIdx - OFFSET], num[childIdx - OFFSET]);
}
}
int idxFromChilds(int* num, int parentIdx, int end, int(*comp)(int, int)) {
int childIdx = parentIdx * 2;
return isRightLeafSuitable(num, childIdx, end, comp) ?
childIdx + 1 : childIdx;
}
int isRightLeafSuitable(int* num, int childIdx,
int end, int(*comp)(int, int)) {
return childIdx < end - 1 &&
comp(num[childIdx + 1 - OFFSET], num[childIdx - OFFSET]) > 0;
}
void print(int* arr, int len) {
int i;
for(i = 0; i < len; i++) { printf("%d ", arr[i]); }
printf("\n");
}
int ascending(int a, int b) { return a - b; }
int descending(int a, int b) { return -ascending(a, b); }
import java.util.*;
import static java.lang.System.out;
import static java.util.Collections.swap;
public class Sort {
public static <T extends Comparable<? super T>>
int ascending(T t1, T t2) { return t1.compareTo(t2); }
public static <T extends Comparable<? super T>>
int descending(T t1, T t2) { return -ascending(t1, t2); }
public static <T extends Comparable<? super T>>
void heapSort(List<T> list) { heapSort(list, Sort::ascending); }
private static final int OFFSET = 1;
public static <T> void heapSort(
List<T> list, Comparator<? super T> c) {
heapTree(list, c);
selectFromHeap(list, c);
}
private static <T> void heapTree(List<T> list, Comparator<? super T> c) {
for(int i = 1, end = list.size() + 1; i < end; i++) {
bubbleLeaf(list, i, c);
}
}
private static <T> void selectFromHeap(List<T> list,
Comparator<? super T> c) {
for(int end = list.size(); end > OFFSET; end--) {
swap(list, 1 - OFFSET, end - OFFSET);
bubbleRoot(list, end, c);
}
}
private static <T> void bubbleLeaf(List<T> list,
int eleIdx, Comparator<? super T> c) {
for(int childIdx = eleIdx, parentIdx = eleIdx / 2;
isBubbleable(list, childIdx, parentIdx, c);
childIdx = parentIdx, parentIdx = childIdx / 2) {
swap(list, parentIdx - OFFSET, childIdx - OFFSET);
}
}
private static <T> boolean isBubbleable(List<T> list, int childIdx,
int parentIdx, Comparator<? super T> c) {
return childIdx > OFFSET && c.compare(
list.get(parentIdx - OFFSET), list.get(childIdx - OFFSET)) < 0;
}
private static <T> void bubbleRoot(List<T> list,
int end, Comparator<? super T> c) {
for(int parentIdx = 0 + OFFSET,
childIdx = idxFromChilds(list, parentIdx, end, c);
childIdx < end &&
c.compare(list.get(childIdx - OFFSET),
list.get(parentIdx - OFFSET)) > 0;
parentIdx = childIdx,
childIdx = idxFromChilds(list, parentIdx, end, c)) {
swap(list, parentIdx - OFFSET, childIdx - OFFSET);
}
}
private static <T> int idxFromChilds(List<T> list,
int parentIdx, int end, Comparator<? super T> c) {
int childIdx = parentIdx * 2;
return isRightLeafSuitable(list, childIdx, end, c) ?
childIdx + 1 : childIdx;
}
private static <T> boolean isRightLeafSuitable(List<T> list,
int childIdx, int end, Comparator<? super T> c) {
return childIdx < end - 1 &&
c.compare(list.get(childIdx + 1 - OFFSET),
list.get(childIdx - OFFSET)) > 0;
}
public static void main(String[] args) {
List<Integer> list =
new ArrayList<>(Arrays.asList(10, 9, 1, 2, 5, 3, 8, 7, 12, 11));
heapSort(list);
out.println(list);
heapSort(list, Sort::descending);
out.println(list);
}
}
def ascending(a, b): return a - b
def descending(a, b): return -ascending(a, b)
__OFFSET = 1
def heapSort(xs, comp = ascending):
if not xs:
return []
else:
heapped = heapTree([], xs, comp)
return selectFromHeap(heapped, [], comp)
def heapTree(heapped, xs, comp):
if not xs:
return heapped
else:
return heapTree(bubbleLeaf(heapped, xs[0], comp), xs[1:], comp)
def bubbleLeaf(heapped, child, comp):
if not heapped:
return [child]
else:
parentIdx = (len(heapped) + 1) // 2
if comp(heapped[parentIdx - __OFFSET], child) < 0:
heappedChilds = (heapped[parentIdx - __OFFSET + 1:] +
[heapped[parentIdx - __OFFSET]])
heappedParents = heapped[0:parentIdx - __OFFSET]
return bubbleLeaf(heappedParents, child, comp) + heappedChilds
else:
return heapped + [child]
def selectFromHeap(heapped, sorted, comp):
if len(heapped) == 1:
return heapped + sorted
else:
rootSorted = [heapped[0]] + sorted
unheapped = [heapped[-1]] + heapped[1:-1]
leftHeapped = bubbleRoot(unheapped, 1, 0, comp)
return selectFromHeap(leftHeapped, rootSorted, comp)
def bubbleRoot(unheapped, parentIdx, heappedLen, comp):
childLIdx = (parentIdx * 2) - heappedLen
if len(unheapped) == 1 or childLIdx > len(unheapped):
return unheapped
else:
childIdx = idxFromChilds(childLIdx, unheapped, comp)
if comp(unheapped[childIdx - __OFFSET], unheapped[0]) > 0:
heapped = ([unheapped[childIdx - __OFFSET]] +
unheapped[1:childIdx - __OFFSET])
rightUnheapped = ([unheapped[0]] +
unheapped[childIdx + 1 - __OFFSET:])
return heapped + bubbleRoot(rightUnheapped,
heappedLen + childIdx,
heappedLen + childIdx - 1, comp)
else:
return unheapped
def idxFromChilds(childLIdx, unheapped, comp):
return (childLIdx + 1 if childLIdx < len(unheapped) and
comp(unheapped[childLIdx + 1 - __OFFSET],
unheapped[childLIdx - __OFFSET]) > 0
else childLIdx)
list = [10, 9, 1, 2, 5, 3, 8, 7, 12, 11]
print(heapSort(list))
print(heapSort(list, descending))
object Sort {
private val OFFSET = 1
def heap[T](xs: List[T], compare: (T, T) => Boolean):List[T] = {
if(xs.isEmpty) Nil
else {
val heapped = heapTree(Nil, xs, compare)
selectFromHeap(heapped, Nil, compare)
}
}
private def heapTree[T](heapped: List[T], xs: List[T],
compare: (T, T) => Boolean): List[T] = {
if(xs.isEmpty) heapped
else {
heapTree(bubbleLeaf(heapped, xs(0), compare), xs.tail, compare)
}
}
private def bubbleLeaf[T](heapped: List[T], child: T,
compare: (T, T) => Boolean): List[T] = {
if(heapped.isEmpty) List(child)
else {
val parentIdx = (heapped.size + 1) / 2
if(compare(child, heapped(parentIdx - OFFSET))) {
val heappedChilds =
heapped.slice(parentIdx - OFFSET + 1, heapped.size)
++ List(heapped(parentIdx - OFFSET))
val heappedParents = heapped.slice(0, parentIdx - OFFSET)
bubbleLeaf(heappedParents, child, compare) ++ heappedChilds
}
else heapped ++ List(child)
}
}
private def selectFromHeap[T](heapped: List[T], sorted: List[T],
compare: (T, T) => Boolean): List[T] = {
if(heapped.size == 1) heapped ++ sorted
else {
val rootSorted = heapped.head :: sorted
val unheapped = heapped.last ::
heapped.slice(1, heapped.size - 1)
val leftHeapped = bubbleRoot(unheapped, 1, 0, compare)
selectFromHeap(leftHeapped, rootSorted, compare)
}
}
private def bubbleRoot[T](unheapped: List[T], parentIdx: Int,
heappedLen: Int, compare: (T, T) => Boolean): List[T] = {
val childLIdx = (parentIdx * 2) - heappedLen
if(unheapped.size == 1 || childLIdx > unheapped.size) unheapped
else {
val childIdx = idxFromChilds(childLIdx, unheapped, compare)
if(compare(unheapped(childIdx - OFFSET), unheapped.head)) {
val heapped = unheapped(childIdx - OFFSET) ::
unheapped.slice(1, childIdx - OFFSET)
val rightUnheapped = unheapped.head ::
unheapped.slice(childIdx + 1 - OFFSET, unheapped.size)
heapped ++ bubbleRoot(rightUnheapped, heappedLen + childIdx,
heappedLen + childIdx - 1, compare)
}
else unheapped
}
}
private def idxFromChilds[T](childLIdx: Int,
unheapped: List[T], compare: (T, T) => Boolean) = {
if(childLIdx < unheapped.size &&
compare(unheapped(childLIdx + 1 - OFFSET),
unheapped(childLIdx - OFFSET))) {
childLIdx + 1
}
else childLIdx
}
}
val list = List(10, 9, 1, 2, 5, 3, 8, 7, 12, 11)
println(Sort.heap[Int](list, _ > _))
println(Sort.heap[Int](list, _ < _))class Sort
@@ascending = ->(a, b) { a - b }
@@descending = ->(a, b) { -@@ascending.call(a, b) }
def self.ascending; @@ascending end
def self.descending; @@descending end
OFFSET = 1
def self.heap(xs, comp)
if xs.empty?
[]
else
heapped = heapTree([], xs, comp)
selectFromHeap(heapped, [], comp)
end
end
def self.heapTree(heapped, xs, comp)
if xs.empty?
heapped
else
heapTree(bubbleLeaf(heapped, xs[0], comp), xs[1..-1], comp)
end
end
private_class_method :heapTree
def self.bubbleLeaf(heapped, child, comp)
if heapped.empty?
[child]
else
parentIdx = (heapped.size + 1) / 2
if comp.call(heapped[parentIdx - OFFSET], child) < 0
heappedChilds = (heapped[parentIdx - OFFSET + 1..-1] +
[heapped[parentIdx - OFFSET]])
heappedParents = heapped[0...parentIdx - OFFSET]
bubbleLeaf(heappedParents, child, comp) + heappedChilds
else
heapped + [child]
end
end
end
private_class_method :bubbleLeaf
def self.selectFromHeap(heapped, sorted, comp)
if heapped.size == 1
heapped + sorted
else
rootSorted = [heapped[0]] + sorted
unheapped = [heapped.last] + heapped[1...-1]
leftHeapped = bubbleRoot(unheapped, 1, 0, comp)
selectFromHeap(leftHeapped, rootSorted, comp)
end
end
private_class_method :selectFromHeap
def self.bubbleRoot(unheapped, parentIdx, heappedLen, comp)
childLIdx = (parentIdx * 2) - heappedLen
if unheapped.size == 1 or childLIdx > unheapped.size
unheapped
else
childIdx = idxFromChilds(childLIdx, unheapped, comp)
if comp.call(unheapped[childIdx - OFFSET], unheapped[0]) > 0
heapped = ([unheapped[childIdx - OFFSET]] +
unheapped[1...childIdx - OFFSET])
rightUnheapped = ([unheapped[0]] +
unheapped[childIdx + 1 - OFFSET..-1])
heapped + bubbleRoot(rightUnheapped,
heappedLen + childIdx,
heappedLen + childIdx - 1, comp)
else
unheapped
end
end
end
private_class_method :bubbleRoot
def self.idxFromChilds(childLIdx, unheapped, comp)
(childLIdx < unheapped.size and
comp.call(unheapped[childLIdx + 1 - OFFSET],
unheapped[childLIdx - OFFSET]) > 0) ?
childLIdx + 1 : childLIdx
end
private_class_method :idxFromChilds
end
list = [10, 9, 1, 2, 5, 3, 8, 7, 12, 11]
print(Sort.heap(list, Sort.ascending).to_s + "\n")
print(Sort.heap(list, Sort.descending).to_s + "\n")
function ascending(a, b) {return a - b;}
function descending(a, b) {return -ascending(a, b);}
var heapSort = function() {
function swap(list, i, j) {
var ele = list[i];
list[i] = list[j];
list[j] = ele;
}
var OFFSET = 1;
function sort(list, c) {
heapTree(list, c);
selectFromHeap(list, c);
}
function heapTree(list, c) {
for(var i = 1, end = list.length + 1; i < end; i++) {
bubbleLeaf(list, i, c);
}
}
function selectFromHeap(list, c) {
for(var end = list.length; end > OFFSET; end--) {
swap(list, 1 - OFFSET, end - OFFSET);
bubbleRoot(list, end, c);
}
}
function bubbleLeaf(list, eleIdx, c) {
for(var childIdx = eleIdx, parentIdx = parseInt(eleIdx / 2);
isBubbleable(list, childIdx, parentIdx, c);
childIdx = parentIdx, parentIdx = parseInt(childIdx / 2)) {
swap(list, parentIdx - OFFSET, childIdx - OFFSET);
}
}
function isBubbleable(list, childIdx, parentIdx, c) {
return childIdx > OFFSET && c(
list[parentIdx - OFFSET], list[childIdx - OFFSET]) < 0;
}
function bubbleRoot(list, end, c) {
for(var parentIdx = 0 + OFFSET,
childIdx = idxFromChilds(list, parentIdx, end, c);
childIdx < end &&
c(list[childIdx - OFFSET], list[parentIdx - OFFSET]) > 0;
parentIdx = childIdx,
childIdx = idxFromChilds(list, parentIdx, end, c)) {
swap(list, parentIdx - OFFSET, childIdx - OFFSET);
}
}
function idxFromChilds(list, parentIdx, end, c) {
var childIdx = parentIdx * 2;
return isRightLeafSuitable(list, childIdx, end, c) ?
childIdx + 1 : childIdx;
}
function isRightLeafSuitable(list, childIdx, end, c) {
return childIdx < end - 1 &&
c(list[childIdx + 1 - OFFSET], list[childIdx - OFFSET]) > 0;
}
return sort;
}();
var list = [10, 9, 1, 2, 5, 3, 8, 7, 12, 11];
heapSort(list, ascending);
print(list);
heapSort(list, descending);
print(list);
ascending a b = a - b
descending a b = -ascending a b
slice from to xs = take (to - from) (drop from xs)
tailFrom from xs = slice from (length xs) xs
initUntil until xs = slice 0 until xs
offset = 1
heapSort xs comp =
if xs == [] then []
else
let heapped = heapTree [] xs comp
in selectFromHeap heapped [] comp
heapTree heapped xs comp =
if xs == []
then heapped
else heapTree (bubbleLeaf heapped (head xs) comp) (tail xs) comp
bubbleLeaf heapped child comp =
if heapped == [] then [child]
else
let parentIdx = (length heapped + 1) `div` 2
in
if (comp (heapped !! (parentIdx - offset)) child) < 0 then
let heappedChilds =
(tailFrom (parentIdx - offset + 1) heapped) ++
[heapped !! (parentIdx - offset)]
heappedParents = initUntil (parentIdx - offset) heapped
in (bubbleLeaf heappedParents child comp) ++ heappedChilds
else
heapped ++ [child]
selectFromHeap heapped sorted comp =
if (length heapped == 1) then heapped ++ sorted
else
let rootSorted = (head heapped) : sorted
unheapped = (last heapped) : (init \$ tail heapped)
leftHeapped = bubbleRoot unheapped 1 0 comp
in selectFromHeap leftHeapped rootSorted comp
bubbleRoot unheapped parentIdx heappedLen comp =
if (length unheapped == 1) || (childLIdx > length unheapped)
then unheapped
else
let childIdx = idxFromChilds childLIdx unheapped comp
in
if comp (unheapped !! (childIdx - offset)) (head unheapped) > 0
then
let heapped = (unheapped !! (childIdx - offset)) :
(slice 1 (childIdx - offset) unheapped)
rightUnheapped =
(head unheapped) :
(tailFrom (childIdx + 1 - offset) unheapped)
in heapped ++
(bubbleRoot rightUnheapped (heappedLen + childIdx)
(heappedLen + childIdx - 1) comp)
else unheapped
where childLIdx = (parentIdx * 2) - heappedLen
idxFromChilds childLIdx unheapped comp =
if childLIdx < (length unheapped) &&
(comp (unheapped !! (childLIdx + 1 - offset))
(unheapped !! (childLIdx - offset))) > 0
then childLIdx + 1
else childLIdx
main = sequence [print \$ heapSort list ascending,
print \$ heapSort list descending]
where list = [10, 9, 1, 2, 5, 3, 8, 7, 12, 11]

