說明
二分搜尋法每次搜尋時,都會將搜尋區間分為一半,所以其搜尋時間為O(log(2)n),log(2)表示以2為底的log值,這邊要介紹的費氏搜尋,其利用費氏數列作為間隔來搜尋下一個數,所以區間收斂的速度更快,搜尋時間為O(logn)。解法
費氏搜尋使用費氏數列來決定下一個數的搜尋位置,所以必須先製作費氏數列,這在之前有提過;費氏搜尋會先透過公式計算求出第一個要搜尋數的位置,以及其代 表的費氏數,以搜尋對象10個數字來說,第一個費氏數經計算後一定是F5,而第一個要搜尋的位置有兩個可能,例如若在下面的數列搜尋的話(為了計算方便, 通常會將索引0訂作無限小的數,而數列由索引1開始):-∞ 1 3 5 7 9 13 15 17 19 20
如果要搜尋5的話,則由索引F5(F5表示第五個費式數作為索引,也就是5)開始搜尋,接下來如果數列中的數大於指定搜尋值時,就往左找,小於時就向右,每次找的間隔是F4(第四個費式數作為索引,也就是3)、F3(第三個費式數作為索引,也就是2)、F2(第二個費式數作為索引,也就是1)來尋找,當費氏數為0時還沒找到,就表示尋找失敗,如下所示:
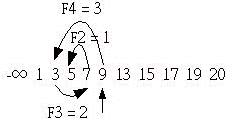
如果要搜尋19,由於第一個搜尋值索引F5處的值小於19,所以此時必須對齊數列右方,也就是將第一個搜尋值的索引改為F5+2 = 7,然後如同上述的方式進行搜尋,如下所示:
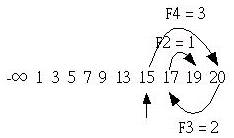
至於第一個搜尋值是如何找到的?我們可以由以下這個公式來求得,其中n為搜尋對象的個數,Fy為第y個費式數,必須大於等於n,若算出x值,則使用Fx作為第一個搜尋索引,也就是第x個費式數:
以10個搜尋對象來說:
取Fy = 8, m = 2,所以可以對照費氏數列得到8是第六個費式數,所以y=6,所以x得5,也就是使用第五個費式數的值(也就是5)作為索引開始搜尋。
如果數列在索引5處的值大於指定的搜尋值,則第一個搜尋位置就是索引5的位置,如果小於指定的搜尋值,則第一個搜尋位置必須加上m,也就是F5 + m = 5 + 2 = 7,也就是索引7的位置,其實加上m的原因,是為了要讓下一個搜尋值剛好是數列的最後一個位置。
費氏搜尋看來難懂,但只要掌握Fy + m = n這個公式,自己找幾個實例算一次,很容易就可以理解;費氏搜尋除了收斂快速之外,由於其本身只會使用到加法與減法,在運算上也可以加快。
Fy + m = n
Fy >= n + 1
x = y - 1
Fy >= n + 1
x = y - 1
以10個搜尋對象來說:
Fy + m = 10
取Fy = 8, m = 2,所以可以對照費氏數列得到8是第六個費式數,所以y=6,所以x得5,也就是使用第五個費式數的值(也就是5)作為索引開始搜尋。
如果數列在索引5處的值大於指定的搜尋值,則第一個搜尋位置就是索引5的位置,如果小於指定的搜尋值,則第一個搜尋位置必須加上m,也就是F5 + m = 5 + 2 = 7,也就是索引7的位置,其實加上m的原因,是為了要讓下一個搜尋值剛好是數列的最後一個位置。
費氏搜尋看來難懂,但只要掌握Fy + m = n這個公式,自己找幾個實例算一次,很容易就可以理解;費氏搜尋除了收斂快速之外,由於其本身只會使用到加法與減法,在運算上也可以加快。
實作:C Java Python Scala Ruby
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define INT_MIN -9999
void createFibonacci(int[], int); // 建立費氏數列
int findY(int[], int); // 找Y值
int fibonacciSearch(int[], int, int); // 費氏搜尋
int main(void) {
int number[] = {1, 2, 3, 5, 6, 8, 9, 10, 11};
int length = sizeof(number) / sizeof(int);
printf("數列:");
int i;
for(i = 0; i < length; i++)
printf("%d ", number[i]);
printf("\n輸入尋找對象:");
int find;
scanf("%d", &find);
if((i = fibonacciSearch(number, length, find)) >= 0)
printf("找到數字於索引 %d ", i);
else
printf("\n找不到指定數");
printf("\n");
return 0;
}
// 建立費氏數列
void createFibonacci(int Fib[], int length) {
Fib[0] = 0;
Fib[1] = 1;
int i;
for(i = 2; i < length; i++)
Fib[i] = Fib[i-1] + Fib[i-2];
}
// 找 y 值
int findY(int Fib[], int n) {
int i = 0;
while(Fib[i] <= n) i++;
i--;
return i;
}
// 費式搜尋
int fibonacciSearch(int number[], int length, int find) {
int* Fib = malloc(length * sizeof(int));
int f;
for(f = 0; f < length; f++) {
Fib[f] = INT_MIN;
}
createFibonacci(Fib, length);
int y = findY(Fib, length + 1);
int m = length - Fib[y];
int x = y - 1;
// printf("\nx = %d, m = %d, Fib[x] = %d\n\n", x, m, Fib[x]);
int i = x;
if(number[i] < find)
i += m;
int result = -1;
while(Fib[x] > 0) {
if(number[i] < find)
i += Fib[--x];
else if(number[i] > find)
i -= Fib[--x];
else {
result = i;
break;
}
}
free(Fib);
return result;
}
public class Search {
public static int fibonacci(int[] number, int des) {
int[] fib = createFibonacci(number.length);
int max = number.length - 1;
int y = findY(fib, max+1);
int m = max - fib[y];
int x = y - 1;
// System.out.printf("\nx=%d, m=%d, fib[x]=%d", x, m, fib[x]);
int i = x;
if(number[i] < des)
i += m;
while(fib[x] > 0) {
if(number[i] < des)
i += fib[--x];
else if(number[i] > des)
i -= fib[--x];
else
return i;
}
return -1;
}
private static int[] createFibonacci(int max) {
int[] fib = new int[max];
for(int i = 0; i < fib.length; i++) {
fib[i] = Integer.MIN_VALUE;
}
fib[0] = 0;
fib[1] = 1;
for(int i = 2; i < max; i++)
fib[i] = fib[i-1] + fib[i-2];
return fib;
}
private static int findY(int[] fib, int n) {
int i = 0;
while(fib[i] <= n) i++;
i--;
return i;
}
public static void main(String[] args) {
int[] number = {1, 2, 3, 5, 6, 8, 9, 10, 11};
int find = Search.fibonacci(number, 2);
System.out.println(find >= 0 ? "找到數值於索引" + find : "找不到數值");
}
} import sys
def search(number, des):
fib = fibonacci(len(number))
max = len(number) - 1
y = findY(fib, max + 1)
m = max - fib[y]
x = y - 1
# print("\nx=%d, m=%d, fib[x]=%d" % (x, m, fib[x]))
i = x
if number[i] < des:
i += m
while fib[x] > 0:
if number[i] < des:
x -= 1
i += fib[x]
elif number[i] > des:
x -= 1
i -= fib[x]
else:
return i
return -1
def fibonacci(max):
fib = [sys.maxsize] * max
fib[0] = 0
fib[1] = 1
for i in range(2, max):
fib[i] = fib[i -1] + fib[i - 2]
return fib
def findY(fib, n):
i = 0
while fib[i] <= n:
i += 1
return i - 1
number = [1, 4, 2, 6, 7, 3, 9, 8]
number.sort()
find = search(number, 3)
print("找到數值於索引 " + str(find) if find >= 0 else "找不到數值")object Search {
def fibonacci(number: Array[Int], des: Int): Int = {
val fib = fibonacci(number.length)
def y(i: Int): Int = if(fib(i) <= number.length) y(i + 1) else i - 1
def search(x: Int, i: Int): Int = {
if(fib(x) > 0 && number(i) != des) {
if(number(i) < des) search(x - 1, i + fib(x - 1))
else search(x - 1, i - fib(x - 1))
} else i
}
val x = y(0) - 1
if(number(x) < des) search(x, x + number.length - 1 - fib(x + 1))
else search(x, x)
}
private def fibonacci(max: Int): Array[Int] = {
def fib(n: Int): Int = n match {
case 0 => 0
case 1 => 1
case _ => fib(n - 1) + fib(n - 2)
}
(for(i <- 0 until max) yield fib(i)).toArray
}
}
val number = Array(1, 2, 3, 4, 6, 7, 8)
val find = Search.fibonacci(number, 3)
println(if(find >= 0) "找到數值於索引 " + find else "找不到數值")
class Integer
N_BYTES = [42].pack('i').size
N_BITS = N_BYTES * 8
MAX = 2 ** (N_BITS - 2) - 1
MIN = -MAX - 1
end
def search(number, des)
fib = fibonacci(number.length)
max = number.length - 1
y = findY(fib, max + 1)
m = max - fib[y]
x = y - 1
i = x
if number[i] < des
i += m
end
while fib[x] > 0
if number[i] < des
x -= 1
i += fib[x]
elsif number[i] > des
x -= 1
i -= fib[x]
else
return i
end
end
-1
end
def fibonacci(max)
fib = Array.new(max, Integer::MAX)
fib[0] = 0
fib[1] = 1
2.upto(max - 1) { |i|
fib[i] = fib[i -1] + fib[i - 2]
}
fib
end
def findY(fib, n)
i = 0
while fib[i] <= n
i += 1
end
i - 1
end
number = [1, 4, 2, 6, 7, 3, 9, 8]
number.sort!
find = search(number, 2)
print find >= 0 ? "找到數值於索引 ".encode("Big5") + find.to_s :
"找不到數值".encode("Big5"), "\n"

