費式數列

說明

Fibonacci為1200年代的歐洲數學家，在他的著作中曾經提到：「若有一隻免子每個月生一隻小免子，一個月後小免子也開始生產。起初只有一隻免子，一個月後就有兩隻免子，二個月後有三隻免子，三個月後有五隻免子（小免子投入生產）......」。

如果不太理解這個例子的話，舉個圖就知道了，注意新生的小免子需一個月成長期才會投入生產，類似的道理也可以用於植物的生長，這就是 Fibonacci數列，一般習慣稱之為費氏數列，例如以下：
1、1 、2、3、5、8、13、21、34、55、89......

解法

依說明，我們可以將費氏數列定義為以下：

F0
            = 0

            F1 = 1

            Fn = Fn-1 + Fn-2

算法

費氏陣列的解法很多，基本上可以使用遞迴解，演算法最簡單，如下：

Procedure FIB(N) 
    IF (N = 0 OR N = 1) 
        RETURN N
    ELSE 
        RETURN FIB(N-1) + FIB(N-2)

簡單，但是不實用，因為太慢了，在求每一個費氏數時，都會發生嚴重的重覆計算，也就是遞迴該行 ( FIB(N-1) + FIB(N-2) )，最差的big-o可以到2的n/2次方，畫張遞迴的樹狀圖就可以知道重覆計算的數有多少了。

可以採取非遞迴的版本，可以將big(o)減至n，演算法如下：

Procedure FIB(N)
    IF (N = 0 OR N = 1) 
        RETURN N

    a = 0; 
    b = 1; 
    FOR i = 2 TO N [
        temp = b; 
        b = a + b; 
        a = temp; 
    ]
    RETURN b; 
]

若想要一次列出所有N之前的費氏數，則可以將for迴圈的部份改以陣列，也就是：

F(0) = 0; 
F(1) = 1; 
FOR i<-2 TO N [
    F(i) = F(i-1) + F(i-2); 
]

費氏陣列並不是使用遞迴來解一定不好，事實上單就執行次數上來說，有一個使用遞迴的演算法可以更快 (big(o)是以2為底的Logn值)，但是要使用到乘法運算，所以實際上要看所使用的機器而定。

Procedure FIB(N) 
    IF (n <= 1)
        RETURN(n); 

    IF (n = 2) 
        RETURN(1); 
    ELSE [ 
        i = n/2; 
        f1 = FIB(i+1); 
        f2 = FIB(i); 

        IF (n mod 2 = 0)
            RETURN( f2*(2*f1+f2) ); 
        ELSE 
            RETURN ( f1**2+f2**2 ); 
    ]
]

您可以實際使用費氏數列來印證演算法中的那兩條公式，其中f1**2表示f1的平方；若將遞迴的樹狀圖畫出來，就像這樣：

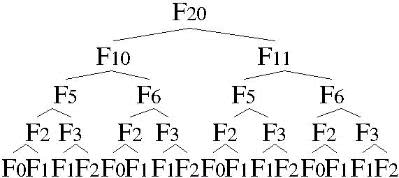
另外費氏數列還有公式解，導證方式就不提了：

您說，如果兔子不只生一隻小兔子的話怎麼辦？像這種問題，我們可以將費氏數列加以擴充，稱之為擴充費氏數列：

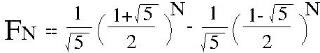
F0
            = 0

            F1 = 1

            Fn = X * Fn-1 + Y * Fn-2

當X、Y等於1時，自然就是一般的費氏數列了。

想瞭解費氏數列與自然界神奇的關係，可以造訪這個網頁。

實作：Toy C Java Python Scala Ruby JavaScript Haskell Prolog

def fib(n) {
    if n == 0 or n == 1 {
        return n
    }
    return fib(n - 1) + fib(n - 2)
}

iterate(0, 10).forEach(i -> println(fib(i)))

#include <stdio.h> 
#include <stdlib.h> 
#define LEN 20 

void fill_fibonacci_numbers(int*, int);
void print(int*, int len);

int main(void) { 
    int fib[LEN] = {0}; 
    
    fill_fibonacci_numbers(fib, LEN);
    print(fib, LEN);

    return 0; 
} 

void fill_fibonacci_numbers(int* fib, int len) {
    fib[0] = 0; 
    fib[1] = 1; 
    int i;
    for(i = 2; i < len; i++) {
        fib[i] = fib[i-1] + fib[i-2]; 
    }
}

void print(int* arr, int len) {
    int i;
    for(i = 0; i < len; i++) { printf("%d ", arr[i]); } 
    printf("\n");
}

Java

import java.util.*;

public class Fibonacci {
    private List<Integer> fib = new ArrayList<>();
    {
        fib.add(0);
        fib.add(1);
    }
    
    Integer get(int n) {
        if(n >= fib.size()) for(int i = fib.size(); i <= n; i++) {
            fib.add(fib.get(i - 1) + fib.get(i - 2));
        }
        return fib.get(n);
    }
    
    public static void main(String[] args) {
        Fibonacci fibonacci = new Fibonacci();
        for(int i = 0; i < 20; i++) {
            System.out.print(fibonacci.get(i) + " ");
        }
    }
}

Python

def fibonacci(n, fib = [0, 1]):
    if n >= len(fib):
        for i in range(len(fib), n + 1):
            fib.append(fib[i - 1] + fib[i - 2])
    return fib[n]

for i in range(0, 20):
    print(fibonacci(i), end=' ')

Scala

def fib(n: Int): Int = n match {
    case 0 => 0
    case 1 => 1
    case _ => fib(n - 1) + fib(n - 2)
}
(for(i <- 0 until readInt) yield fib(i)).foreach(i => print(i + " "))

Ruby

# encoding: Big5
fibonacci = -> {
    fib = [0, 1]
    -> n { 
        if n >= fib.size
            fib.size.upto(n) do |i|
                fib << fib[i - 1] + fib[i - 2]
            end
        end
        fib[n]
    }
}.call

print "輸入個數："
length = gets.to_i
0.upto(length - 1) do |i|
    print fibonacci.call(i).to_s + ' '
end

JavaScript

var fibonacci = function() {
    var fib = [0, 1];
    return function(n) {
        if(n >= fib.length) for(var i = fib.length; i <= n; i++) {
            fib[i] = fib[i - 1] + fib[i - 2];
        }
        return fib[n];
    };
}();
    
for(var i = 0; i < 20; i++) { print(fibonacci(i)); }

Haskell

fibonacci 0 = 0
fibonacci 1 = 1
fibonacci n = addPrevsRecusivelyUntilCounterIsN (fib 1) (fib 0) 2 n

addPrevsRecusivelyUntilCounterIsN prev1 prev2 counter n
    | counter == n = result
    | otherwise = addPrevsRecusivelyUntilCounterIsN result prev1 (counter + 1) n
    where result = prev1 + prev2

main = sequence [print (fibonacci i) | i <- [0..19]]

Prolog

fibonacci(0, 0).
fibonacci(1, 1).
fibonacci(N, Result) :- NP1 is N - 1, NP2 is N - 2, 
                        fibonacci(NP1, FP1), fibonacci(NP2, FP2), 
                        Result is FP1 + FP2.
  
main([Arg0|_]) :-
        atom_number(Arg0, N),
        fibonacci(N, Result),
        writef("The nth %n is %d\n", [Arg0, Result]).