八個皇后

 說明

解法

所以檢查時，先判斷是否在已放置皇后的可行進方向上，如果沒有再行放置下一個皇后，如此就可大大減少遞迴的次數，例如以下為修剪過後的遞迴檢 查行進路徑：

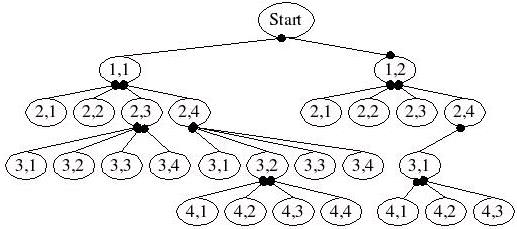
八個皇后的話，會有92個解答，如果考慮棋盤的旋轉，則旋轉後扣去對稱的，會有12組基本解。 

實作：Toy    C    Java    Python    Scala    Ruby    JavaScript    Haskell    Prolog

• Toy

from '/lib/math' import abs

def queenss(n) {
    def placeQueens(k) {
       if k == 0 {
           return [[]]
       }

       def collect(queens) {
           (return range(1, n + 1).filter(column -> isSafe([k, column], queens))
                                  .map(column -> queens.concat([[k, column]]))
                                  .reduce((acc, qs) -> acc.concat([qs]), []))
       }       

       return placeQueens(k - 1).reduce((acc, queens) -> acc.concat(collect(queens)), [])
    }

    return placeQueens(n)
}

def isSafe(queen, queens) {
    return queens.all(q -> not inCheck(queen, q))
}

def inCheck(q1, q2) {
    (return q1.get(0) == q2.get(0) or 
            q1.get(1) == q2.get(1) or 
            abs(q1.get(0) - q2.get(0)) == abs(q1.get(1) - q2.get(1))) 
}

def printQS(qs) {
    qs.forEach(print)
    println()
}

queenss(8).forEach(printQS)

• C

#include <stdio.h> 
#include <stdlib.h> 
#define N 8 

void backTrack(int*, int*, int*, int*, int, void (*)(int*));
void print(int*);

int main(void) { 
    int column[N] = {0};        // 同行是否有皇后
    int slash[2 * N] = {0};     // 右上至左下是否有皇后 
    int backSlash[2 * N] = {0}; // 左上至右下是否有皇后 
    int queens[N] = {0}; 

    backTrack(column, slash, backSlash, queens, 0, print); 
    
    return 0; 
} 

void backTrack(int* column, int* slash, int* backSlash, 
               int* queens, int i, void (*take)(int*)) { 
    if(i >= N) { 
        take(queens); 
    } 
    else { 
        int j;
        for(j = 0; j < N; j++) {
            if(isVisitable(i, j, column, slash, backSlash)) { 
                queens[i] = j; 
                column[j] = slash[i + j] = backSlash[i - j + N] = 1; 
                backTrack(column, slash, backSlash, queens, i + 1, take); 
                column[j] = slash[i + j] = backSlash[i - j + N] = 0;
            } 
        }
    }
}

int isVisitable(int i, int j, int* column, int* slash, int* backSlash) {
   return !(column[j] || slash[i + j] || backSlash[i - j + N]);
}

void print(int* queens) {
    int x, y;
    for(y = 0; y < N; y++) {
        for(x = 0; x < N; x++) {
            printf(" %c", queens[y] == x ? 'Q' : '.');
        }
        printf("\n");
    }
    printf("\n");
}

• Java

import java.util.*;
import static java.lang.Math.abs;
import static java.lang.System.out;

class Queen {
    final int x, y;
    Queen(int x, int y) {
        this.x = x;
        this.y = y;
    }
    
    public String toString() {
        return String.format("(%d, %d)", x, y);
    }
}

public class Queens {
    public static List<List<Queen>> queens(int n) {
        return placeQueens(n, n);
    }
    
    public static List<List<Queen>> placeQueens(int n, int k) {
        List<List<Queen>> queensList = new ArrayList<>();
        if(k == 0) {
            queensList.add(new ArrayList<Queen>());
        }
        else {
            for(List<Queen> queens : placeQueens(n, k - 1)) {
                for(int column = 1; column <= n; column++) {
                    Queen queen = new Queen(k, column);
                    if(isSafe(queen, queens)) {
                        List<Queen> qs = new ArrayList<>();
                        qs.addAll(queens);
                        qs.add(queen);
                        queensList.add(qs);
                    }
                }
            }
        }
        return queensList;
    }
    
    public static boolean isSafe(Queen queen, List<Queen> queens) {
        for(Queen q : queens) if(inCheck(queen, q)) {
            return false;
        }
        return true;
    }
    
    public static boolean inCheck(Queen q1, Queen q2) {
        return q1.x == q2.x || // 同列
               q1.y == q2.y || // 同行
               abs(q1.x - q2.x) == abs(q1.y - q2.y); // 對角線
    }
    
    public static void main(String[] args) {
        for(List<Queen> queens : queens(8)) {
            for(Queen queen : queens) {
                out.print(queen);
            }
            out.println();
        }
    }
}

• Python

def queenss(n):
    def placeQueens(k):
        return [[]] if k == 0 \
                    else [[(k, column)] + queens 
                             for queens in placeQueens(k - 1)
                                 for column in range(1, n + 1) 
                                     if isSafe((k, column), queens)]
    return placeQueens(n)

def isSafe(queen, queens):
    return all(not inCheck(queen, q) for q in queens)

def inCheck(q1, q2):
    return (q1[0] == q2[0] or # 同列
            q1[1] == q2[1] or # 同行
            abs(q1[0] - q2[0]) == abs(q1[1] - q2[1])) # 對角線

for qs in queenss(8):
    for q in qs:
        print(q, end="")
    print()

• Scala

def queens(n: Int): List[List[(Int, Int)]] = {
    def placeQueens(k: Int): List[List[(Int, Int)]] = {
        if(k == 0) Nil
        else for {
                 queens <- placeQueens(k - 1)
                 column <- 1 to n
                 queen = (k, column)
                 if isSafe(queen, queens)
             } yield queen :: queens
    }
    placeQueens(n)
}

def isSafe(queen: (Int, Int), queens: List[(Int, Int)]) =
    queens forall (q => !inCheck(queen, q))
    
def inCheck(q1: (Int, Int), q2: (Int, Int)) =
    q1._1 == q2._1 || // 同列
    q1._2 == q2._2 || // 同行
    (q1._1 - q2._1).abs == (q1._2 - q2._2).abs // 對角線

queens(8).foreach(q => {
    q.foreach(print)
    println()
})

• Ruby

def queenss(n)
    placeQueens(n, n)
end

def placeQueens(n, k)
    k == 0 ? [[]] : placeQueens(n, k - 1).map { |queens|
            (1..n).map { |column| {x: k, y: column} }
                  .find_all { |queen| isSafe(queen, queens) }
                  .map { |queen| [queen] + queens } 
        }.reduce(:+);
end

def isSafe(queen, queens)
    queens.all? { |q| !inCheck(queen, q) }
end

def inCheck(q1, q2)
    q1[:x] == q2[:x] or # 同列
    q1[:y] == q2[:y] or # 同行
    (q1[:x] - q2[:x]).abs == (q1[:y] - q2[:y]).abs # 對角線
end

queenss(8).each do |qs|
    qs.each do |q|
        print "(#{q[:x]}, #{q[:y]})"
    end
    puts
end

• JavaScript

var queens = function() {
    var column = [];
    var slash = [];
    var backSlash = [];
    var queens = [];
    
    function backTrack(n, i, take) {
        if(i >= n) {
            take(n, queens);
        }
        else {
            for(var j = 0; j < n; j++) if(isVisitable(i, j, n)) {
                queens[i] = j;
                column[j] = slash[i + j] = backSlash[i - j + n] = 1; 
                backTrack(n, i + 1, take); 
                column[j] = slash[i + j] = backSlash[i - j + n] = 0;
            }
        }
    }
    
    function isVisitable(i, j, n) {
        return !(column[j] || slash[i + j] || backSlash[i - j + n]);
    }
    
    return function(n, take) {
        backTrack(n, 0, take);
    };
}();

queens(8, function(n, qs) {
    var layout = '';
    for(var y = 0; y < n; y++) {
        for(var x = 0; x < n; x++) {
            layout += (qs[y] === x) ? ' Q' : ' .';
        }
        layout += '\n';
    }
    print(layout);
});

• Haskell

queens n = placeQueens n
    where placeQueens k = 
              if k == 0 then [[]]
              else [(k, column) : queens | queens <- placeQueens (k - 1), 
                                           column <- [1..n], 
                                           isSafe (k, column) queens]
          isSafe queen queens = all (\q -> not \$ inCheck queen q) queens
          inCheck (q1x, q1y) (q2x, q2y) = q1x == q2x || 
                                          q1y == q2y ||
                                          abs (q1x - q2x) == abs (q1y - q2y)

main = sequence [print qs | qs <- queens 8]

• Prolog

line([X, _], [X, _]) :- !.
line([_, Y], [_, Y]) :- !.
line([Qx1, Qy1], [Qx2, Qy2]) :-
    Dx is abs(Qx1 - Qx2), Dy is abs(Qy1 - Qy2), Dx =:= Dy.
    
safe(Q, [H|T]) :- not(line(Q, H)), !, safe(Q, T).
safe(_, []).

range(From, To, Xs) :- findall(X, between(From, To, X), Xs).

forY([Y|T], X, Queens, [NQueens|QueensLt]) :- 
    safe([X, Y], Queens), !,
    NQueens = [[X, Y]|Queens], 
    forY(T, X, Queens, QueensLt).
forY([_|T], X, Queens, QueensLt) :- 
    forY(T, X, Queens, QueensLt).
forY([], _, _, []).

forQueens([HQueens|T], X, Ys, QueensLt) :-
    forQueens(T, X, Ys, TQueensLt), !, 
    forY(Ys, X, HQueens, HQueensLt), 
    append(TQueensLt, HQueensLt, QueensLt).
forQueens([], _, _, []).

forX([X|T], Ys, QueensLt) :- 
    forX(T, Ys, TQueensLt), !, 
    forQueens(TQueensLt, X, Ys, QueensLt).
forX([], _, [[]]).

queens(N, QueensLt) :-
    range(1, N, Xs), 
    range(1, N, Ys),
    forX(Xs, Ys, QueensLt).
    
printQueens([Queen|T]) :- write(Queen), printQueens(T).
printQueens([]) :- nl.

printQueensLt([Queens|T]) :- printQueens(Queens), printQueensLt(T).
printQueensLt([]) :- nl.

main(_) :- 
    queens(8, QueensLt),
    printQueensLt(QueensLt).